5-я международная Иранская олимпиада по геометрии, 2018 год, первая лига, 9-10 классы
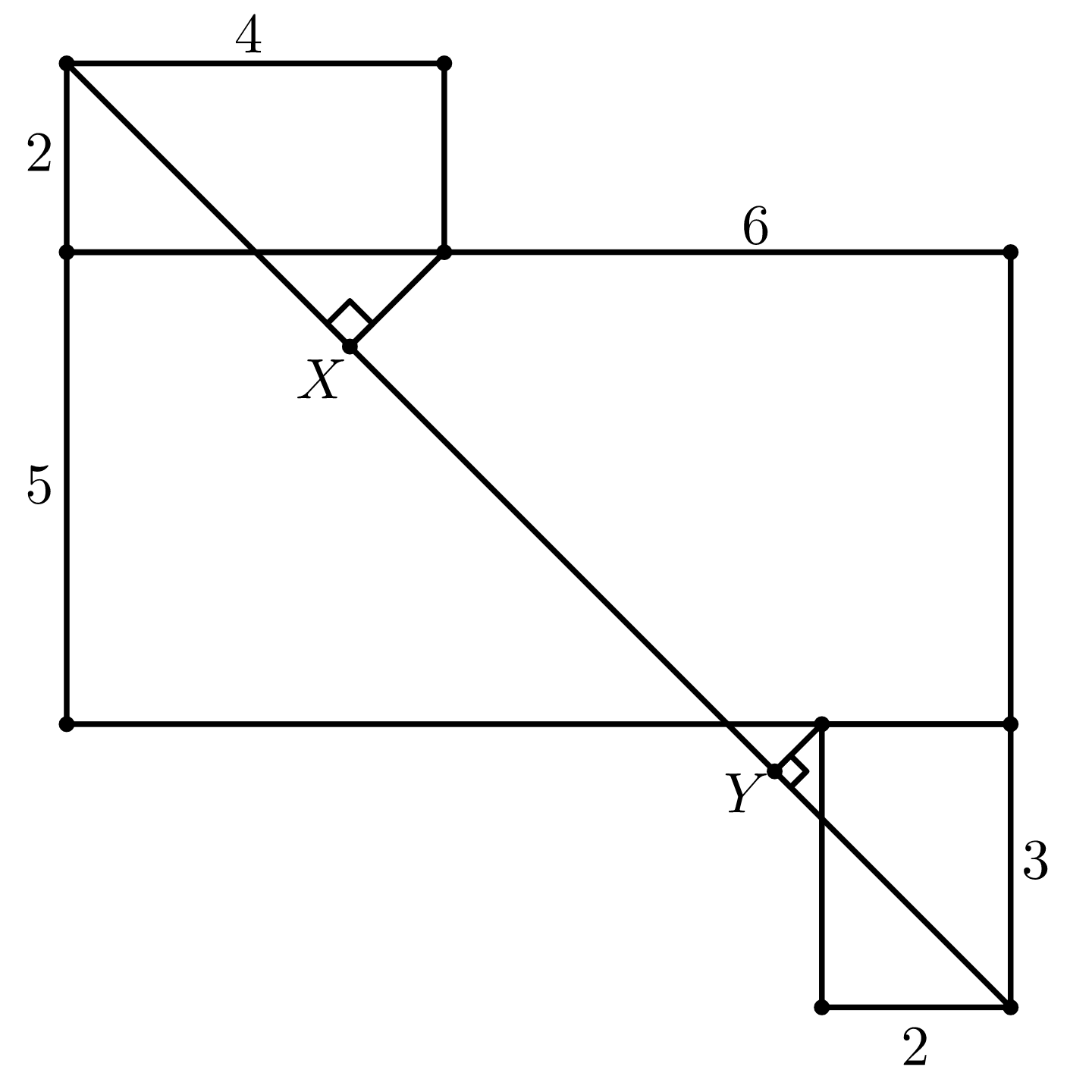
Задача №1. Фигура на рисунке состоит из трех прямоугольников. Возле некоторых из отрезков подписаны их длины. Найдите длину отрезка $XY$.
комментарий/решение(2)
комментарий/решение(2)
Задача №2. Диагонали $AC$ и $BD$ выпуклого четырехугольника $ABCD$ пересекаются в точке $P$. Известно, что $\angle DAC = 90^\circ$ и $2\angle ADB = \angle ACB$.
Докажите, что если $\angle DBC + 2\angle ADC = 180^\circ$, то $2AP = BP$.
комментарий/решение(5)
комментарий/решение(5)
Задача №3. Окружности $\omega_1$ и $\omega_2$ с центрами $O_1$ и $O_2$ соответственно пересекаются в точках $A$ и $B$. Прямая $O_1B$ вторично пересекает окружность $\omega_2$ в точке $C$, прямая $O_2A$ вторично пересекает окружность $\omega_1$ в точке $D$. Пусть $X$ — вторая точка пересечения $AC$ и $\omega_1$, а $Y$ — вторая точка пересечения $BD$ и $\omega_2$.
Докажите, что $CX = DY$.
комментарий/решение(1)
комментарий/решение(1)
Задача №4. Дан многогранник с треугольными гранями. Пусть $P$ — произвольная точка, лежащая на его ребре, причем $P$ не совпадает ни с серединой, ни с концами этого ребра. Положим $P_0=P$. На каждом шаге точка $P_i$ соединяется с центром масс одной из двух граней, содержащих точку $P_i$. Через $P_{i+1}$ обозначим вторую точку пересечения полученной прямой с границей этой грани. Продолжим этот процесс для точки $P_{i+1}$ и другой грани, содержащей $P_{i+1}$. Докажите, что, действуя подобным образом, пересечь все грани многогранника не удастся.
(Центр масс треугольника — это точка пересечения его медиан.)
комментарий/решение
комментарий/решение
Задача №5. Про параллелограмм $ABCD$ известно, что $\angle DAC = 90^\circ$.
Пусть $H$ — основание перпендикуляра, опущенного из $A$ на $DC$, $P$ — такая точка на прямой $AC$, что прямая $PD$ касается описанной окружности треугольника $ABD$. Докажите, что $\angle PBA = \angle DBH$.
комментарий/решение(2)
комментарий/решение(2)