3-я олимпиада им. Шалтая Смагулова, 7 класс, 3 тур, 2019 г.

Задача №1.  Существует ли перестановка $a_1, a_2, a_3, \ldots, a_{30}$ чисел $1,2,3, \ldots, 30$ такая, что число $a_k+k$ является полным квадратом для каждого $k$ от 1 до 30?
комментарий/решение(1)

---

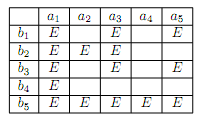
Задача №2.  Умножая на калькуляторе, мальчик заметил, что если произведение больше миллиарда, то калькулятор выдает ответ «$E$». Он взял 10 натуральных чисел: $a_1, a_2, a_3, a_4, a_5$, $b_1, b_2, b_3, b_4, b_5$ и составил «таблицу умножения», в которой отметил все результаты, равные $E$. Докажите, что при составлении таблицы он ошибся.

комментарий/решение(3)

---

Задача №3.  По кругу расставлены сто чисел. Для каждого числа подсчитывают сумму 50 чисел, следующих за ним по часовой стрелке. Затем исходные числа стирают, а вместо них записывают вычисленные суммы. Докажите, что после многократного повторения этой операции все числа станут четными.
комментарий/решение

---

Задача №4.  Назовём два треугольника $ABC$ и $A_1B_1C_1$ почти равными, если $AB=A_1B_1$, $BC=B_1C_1$ и $\angle A=\angle A_1$.
   а) Даны два почти равных треугольника. Верно ли что эти треугольники равны?
   б) Даны три попарно почти равных треугольника. Верно ли, что среди них какие-то два треугольника обязательно равны?
комментарий/решение(2)

---

Задача №5.  Пусть $[x,y]$ означает НОК чисел $x$ и $y$, а $[x,y,z]$ — НОК чисел $x,y,z$. Даны натуральные числа $a,b,c,d$. Обозначим $A=[a,b,c] \cdot [a,b,d] \cdot [a,c,d] \cdot [b,c,d]$ и $B=[a,b] \cdot [a,c] \cdot [a,d] \cdot [b,c] \cdot [b,d] \cdot [c,d]$. Докажите неравенство $A^6 \ge B^4$.
комментарий/решение(1)

---