Республиканская олимпиада по математике, 2014 год, 10 класс

Около неравнобедренного треугольника $ABC$ описана окружность $\omega$, точка $M$ — середина $AC$. Касательная к $\omega$ в точке $B$ пересекает прямую $AC$ в точке $N$, а прямая $BM$ повторно пересекает $\omega$ в точке $L$. Пусть точка $P$ симметрична точке $L$ относительно $M$. Окружность, описанная около треугольника $BPN$, повторно пересекает прямую $AN$ в точке $Q$. Докажите, что $\angle ABP = \angle QBC$. ( М. Кунгожин )

Комментарий/решение

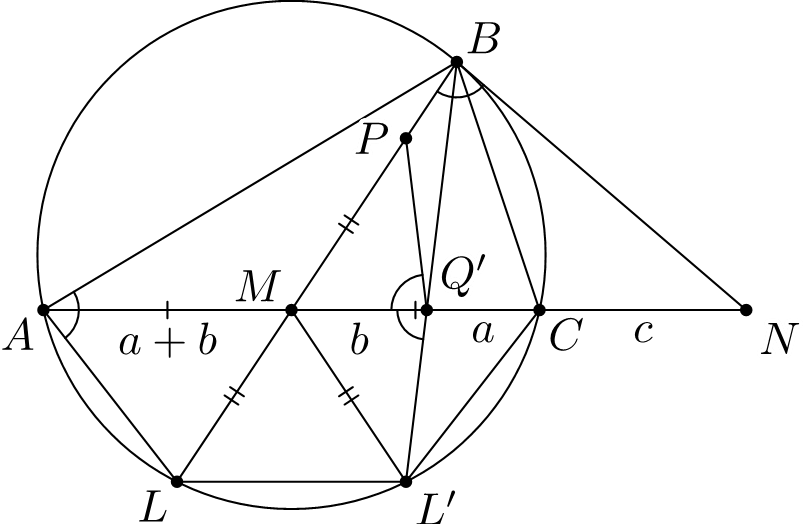
Комментарии от администратора Комментарии от администратора №1.     Не теряя общности положим $AB > BC$. Пусть точка $L'$ на $\omega$ такая, что $LL' \parallel AC$. Обозначим $Q'=BL' \cap AC$. Тогда $AL = CL'$ и $\angle ABL = \angle L'BC = \angle Q'BC$.
Легко заметить, что $\triangle AML = \triangle CML'$. Поэтому $MP = ML = ML'$, откуда $\triangle MPQ' = \triangle ML'Q'$.
Значит, $$\angle PQ'M = \angle MQ'L' = 180^\circ - \angle LL'B = \angle LAB = \angle LBN,$$ т. е. точки $P$, $B$, $N$ и $Q'$ лежат на одной окружности. Осталось заметить, что точки $Q'$ и $Q$ совпадают, так как описанная окружность треугольника $BPN$ пересекает прямую $AN$ не более чем в двух точках.

Комментарии от администратора Комментарии от администратора №2.     $\textit{(Решение Аубекерова Данияра, г. Алматы)}$

Поскольку $PM = ML$ и $AM = MC$, то четырехугольник $APCL$ - параллелограмм. Тогда $\angle CBN = \angle CLB = \angle APL$ и $\angle CBL = \angle LAC = \angle PCA$. Поскольку $\angle CBN + \angle CBL = \angle PBN = \angle PQA$, то $\angle CPQ = \angle PQA - \angle PCA = \angle CBN + \angle CBL - \angle PCA = \angle CBN = \angle APL$. Значит $PM$ и $PQ$ изогональные относительно угла $APC$. Значит $(\frac{AP}{PC})^2 = \frac{AM*AQ}{MC*QC}$ . Чтобы доказать равенство $\angle ABP = \angle QBC$, нам достаточно доказать что $BM$ и $BQ$ изогональные относительно угла $ABC$ , то есть равенство $(\frac{AB}{BC})^2 = \frac{AM*AQ}{MC*QC}$ . Поскольку $(\frac{LC}{AL})^2=(\frac{AP}{PC})^2=\frac{AM*AQ}{MC*QC}$, то нам достаточно доказать, что $\frac{LC}{AL} = \frac{AB}{BC}$.

$\textbf{Лемма:}$ Дан треугольник $ABC$. Пусть точка $M$ середина стороны $AC$ и $BM$ повторно пересекает описанную окружность треугольника $ABC$ в точке $L$. Тогда $\frac{LC}{AL} = \frac{AB}{BC}$.

$\textbf{Доказательство:}$ В треугольнике $ABC$: $\frac{\sin\angle CBM}{\sin\angle ABM} = \frac{AB}{CB}$. В треугольнике $ALC$: $\frac{\sin\angle CBM}{\sin\angle ABM} = \frac{\sin\angle CAL}{\sin\angle ACL} = \frac{LC}{LA}$. Следовательно, $\frac{LC}{AL} = \frac{AB}{BC}$.

Вернемся к задаче. Из вышеуказанной леммы следует что $\frac{LC}{AL} = \frac{AB}{BC}$ что требовалось доказать.

может быть верно

Решение, которое не требует особых знаний,чтобы понять:

Сначало заметим то, что для того, чтобы решить задачу достаточно доказать, что $\angle{ABQ}=\angle{PBC}$. Так как $\angle{QBP}$-общий угол, и на равенство не влияет.

$APCL$-паралелограмм, т.к. $AM=MC;MP=ML$

Назовем углы

$\angle{ACL}=a;\angle{PCA}=x;\angle{PLC}=c$

Разобрав параллельность и углы которые смотрят на одну дугу поймём, что

$\angle{ABL}=\angle{ACL}=\angle{PAC}=a \\ \angle{PCA}=\angle{CAL}=\angle{LBC}=x \\ \angle{BLC}=\angle{BAC}=c \\ \angle{LPC}=180°-a-c-x \Rightarrow \angle{BPC} \Rightarrow \angle{BCP}=180°-a-c-2x \Rightarrow \angle{NBP}=\angle{NBL}=\angle{BCL}=\angle{BCP}+\angle{PCA}+\angle{ACL}=180°-a-c-2x+x+a=180°-c-x$

Из того, что $NBPQ$-вписанный следует, что $\angle{NBP}+\angle{NQP}=180° \Rightarrow \angle{NQP}=c+x \Rightarrow \angle{PQC}=180°-c-x$

Теперь отметим точку $K$ на дуге $AC$ так, чтобы $KC=AL=PC$ и чтобы $K$ лежал в той же полуплоскости что и $L$ относительно прямой $AC$

Тогда заметим, что $\angle{ACL}=\angle{KAC}=a$ Т.к. смотрят на равные дуги, и вписаны.

Значит $\angle{KLC}=180°-\angle{KAC}=180°-x=180°-\angle{ACL}=\angle{AKL} \Rightarrow ACKL$-равнабокая трапеция. От чего $\angle{LAC}=\angle{ACK}=x=\angle{PCA}$ Если учесть, что$CK=CP$ и то, что $QC$ общая сторона и $\angle{ACP}=\angle{ACK} \Leftrightarrow \angle{KCQ}=\angle{QCP}$ то следует, что $\triangle{QPC}=\triangle{QKC} \Rightarrow \angle{QKC}=\angle{QPC}=180°-\angle{PQC}-\angle{PCQ}=180°-(180°-c-x)-x=c$

Так же заметим, что $\angle{BAC}=\angle{BKC}=c$ т.к. смотрят на одну дугу.

Значит $\angle{BKC}=\angle{QKC} \Rightarrow B;Q;K$ лежат на одной прямой.

Тогда $\angle{ABQ}=\angle{ABK}=\angle{AKC}=x=\angle{LBC}=\angle{PBC}$ ЧТД

Очевидно $P$-точка шалтая по лемме и $NB=NP$.Пусть $BS$ симедиана.Докажем что $Q=S$.$\angle NBS=\angle BMA$.$(!) \angle NPS=\angle BMA=\angle PMN$ чтобы BPSN был вписанным.$(!) NA*NC=NB²=NP²=NS*NM$ или

$NM/NA=NC/NS$.$AM/NA=CS/NS$.Это можно доказать через ratio lemma

для треугольников $NBM$ и $NBC$.

P.S. леммы очевидные лемма 2 из Geoma chalka.Доказательств не надо.

Кажется вы ошиблись P-точка шалтая

Что за geoma chalka?

Хорошое решение. Вы чалили EGMO?

Пусть $NK$ - вторая касательная из точки $N$ к $\omega$. Тогда $ABCK$ - гармонический. Остается доказать что $B,Q,K$ лежат на одной прямой.

По степени точки $M$ относительно $\omega$ и $(BPQN)$ выходит:

$MA^2=MA*MC=ML*MB=MP*MB=MQ*MN$ . То есть

$MA^2=MP*MB=MQ*MN$.

Так как $ABCK$ - гармонический, выходит что $\angle ACK=\angle CAL \Rightarrow AK=CL$.

Тогда легко вывести $MK=ML=MP$ , $\angle AMK=\angle CML$.

$\angle AMK=\angle CML=\angle AMP, MP=MK, \Rightarrow \triangle NMP=\triangle NMK, \Rightarrow \angle NPM=\angle NKM,NP=NK=NB$

Совершим инверсию с центром в точке $M$ и радиусом $MA$.Заметим что тогда $B$ перейдет в $P$, $Q$ в $N$,$K$ пусть в $K’$.При инверсии верно что прямая не проходящая через центр инверсии переходит в окружность проходящая через центр инверсии(Верно и обратное утверждение). Тогда чтобы доказать что $B,Q,K$ на одной прямой , достаточно показать что $NPMK’$ вписанный.

$MK*MK’=MP*MB , MP=MK \Rightarrow MB=MK,BP=KK’$

$\angle NPM=\angle NPK \Rightarrow \angle NPB=\angle NKK’$

$\angle NPB=\angle NKK’,NP=NK,PB=KK’ \Rightarrow \triangle NPB=\triangle NKK’ \Rightarrow NK’=NK=NP=NB$.Следовательно:

$\angle NK’K=\angle NKK’=180- \angle NKM=180- \angle NPM \Rightarrow NK’MP$- вписанный.

Проводим вторую касательную тогда это будет отражение точки шалтая и дополнение Гармонического четырехугольника и через равенство доказываем что NP=NB. Совершим Инверсию с центром N и с радиусом NB, и заметим что B перейдет в B и P перейдет в P отсюда (BNPQ) перейдет в BP. Заметим что после инверсии образ точки M будет лежать на (BPQN) и лежать на луче NM , и образ точки N будет лежать на пересечение луча NQ и BP отсюда при совершение иверсии М перейдет в Q и наоборот отсюда NB^2=NQ*NM$ что достаточно для доказательства.

Совершим инверсию с центром $B$ радиусом $\sqrt {AB*BC}$ и симметрией относительно внутриней бисектрисе. Тогда $(ABC)=>AC , N=>N’ , P=>P’$, и заметим что $N’$ лежит на $(ABC)$ и $N’B||AC$ а $P’$ это пересечение касательный из $A$ и $C$ тк $P$ точка шалтая и $(ABP)$ и $(CPB)$ касаются $AC$.Заметим что надо доказать что $Q$ это основание симедианы но ее образ при этой инверсии это $L$ если это так значит докажем что N’-L-P’ коллинеарны тогда по свойству инверсии задача будет решена.

Пусть $N’P’ \cap (ABC)=L_1$ тогда $\angle N’BA=\angle BAC=\angle BL_1C=\angle N’L_1A$ отсюда $L_1=L$

Pamolan не одобряет.