Олимпиада имени Леонарда Эйлера2014-2015 учебный год, I тур заключительного этапа

В треугольнике $ABC$ сторона $AB$ больше стороны $BC$. На продолжении стороны $BC$ за точку $C$ отметили точку $N$ так, что $2BN = AB+BC$. Пусть $BS$ — биссектриса треугольника $ABC$, $M$ — середина стороны $AC$, а $L$ — такая точка на отрезке $BS$, что $ML \parallel AB$. Докажите, что $2LN = AC$. ( А. Антропов )

Комментарий/решение

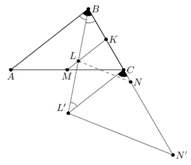
Комментарии от администратора Комментарии от администратора №1.     Продлим $BN$ за $N$ и $BL$ за $L$ на отрезки $NN' = BN$ и $LL' = BL$ соответственно. Так как $M$ — середина $AC$ и $ML \parallel AB$, прямая $ML$ содержит среднюю линию $MK$ треугольника $ABC$. Поскольку $L$ — середина $BL'$, эта прямая содержит также среднюю линию $LK$ треугольника $BCL'$; итак, $CL' \parallel LM \parallel AB$. Поэтому $\angle CL'B = \angle L'BA = \angle L'BC$, откуда $CL' = CB$. Далее, $CN' = BN'-BC = 2BN-BC = BA$ и $\angle N'CL' = \angle CBA$. Значит, треугольники $N'CL'$ и $ABC$ равны, и потому $AC = N'L' = 2LN$.

продлим ML до пересечения с BC и назовем точку как K тогда если угол SBC это a то

угол MLтакже a тогда вертикальный угол такой же и тогда LK=BK на отрезке AB отметим такую точку V что BV=BK тогда BS перпендикулярна KV достроим треугольник

LKV до параллелограма LKVZ заметим что точка Z лежит на отрезке AB по правилу параллельности тогда заметим равенство треугольников KBL и KLC тогда CL=VK=LZ

заметим что угол ZMN 180 тогда эти три точки лежат на одной линий тогда LM средняя линия то есть ML=CN и тогда по SAS MLC и LCN тогда LN=MC а 2MC=AC=2LN ч.т.д

Пусть прямая $ML$ пересекает $BC$ в точке $D$. Так $AB \parallel MD \longrightarrow BD=DC$, и $\angle ABS=\angle BLD=\angle SBD \longrightarrow LD=BD=DC.$ Тогда $2BN=2CN+2BC=2CN+4LD=AB+BC=2MD+2BD=2ML+2LD+2LD=2ML+4LD \rightarrow ML=CN \longrightarrow MD=DN$

$\angle DMN=\angle DNM$ и $\angle DLC=\angle DCL \Longrightarrow \angle MLC=\angle NCL$. Четырехугольник $\square MLCN$ вписанный трапеция, так как $360^\circ=\angle LMN+\angle CNM+\angle MLC+\angle NCL=2\angle LMN+2\angle NCL \Longrightarrow \angle LMN+\angle MLC=\angle LMN+\angle NCL=180^\circ \Longrightarrow$ $LN=MC=\dfrac{1}{2}AC$

ч.т.д.

Введем барицентрическую систему координат $:$

\[A_{(1,0,0)} \ B_{(0,1,0)} \ C_{(0,0,1)} \ M_{\left (\frac{1}{2}, 0, \frac{1}{2} \right )}\ S_{\left (\frac{a}{a+c}, 0, \frac{c}{a+c} \right ) }\ N_{\left (0, \frac{a-c}{2a}, \frac{a+c}{2a} \right )} \]

$L \ $ лежит на $\ BS \ $ и $\ LM \parallel AB :$

\[L_{(a:x:c)} \ \ \text{ и } \ \ L_{\left (y,z,\frac{1}{2} \right) }\ \Rightarrow \ \ L_{\left (\frac{a}{2c}, \frac{c-a}{2c}, \frac{1}{2}\right )}\]

Следовательно $:$

\[ \overrightarrow{ LN }= {\left (\frac{a}{2c}, \frac{c^2-a^2}{2ac}, \frac{-c}{2a} \right )} = (x,y,z)\]

Посчитаем длинну $:$

\[ \lvert LN \rvert = LN^2 = -a^2yz - b^2xz -c^2xy\]

Подставим $:$

\[-a^2\cdot \frac{(c^2-a^2)\cdot (-c)}{4a^2c} - b^2 \cdot\frac{-ac}{4ac}-c^2\cdot \frac{(c^2-a^2)\cdot a}{4ac^2}=\frac{b^2}{4}\]

Тогда $:$

\[LN^2 =\frac{b^2}{4} \ \Leftrightarrow \ LN = \frac{b}{2} \quad \blacksquare\]

Вам надо удалить аккаунт

А за такое решение можно получить дисквал?

Молодец продолжай изучать барики!

Лол