Республиканская олимпиада по математике, 2014 год, 11 класс


В неравнобедренном треугольнике $ABC$ вписанная окружность касается сторон $AB$ и $BC$ в точках $C_1$ и $A_1$ соответственно, а вневписанная окружность (касающаяся стороны $AC$) — соответственно в точках $C_2$ и $A_2$. Точка $N$ — основание биссектрисы из вершины $B$. Прямая $A_1C_1$ пересекают прямую $AC$ в точке $K_1$. Пусть описанная окружности треугольника $BK_1N$ повторно пересекают описанную окружность треугольника $ABC$ в точке $P_1$. Аналогично определим точки $K_2$ и $P_2$. Докажите, что $AP_1 = CP_2$. ( М. Кунгожин )
посмотреть в олимпиаде

Комментарий/решение:

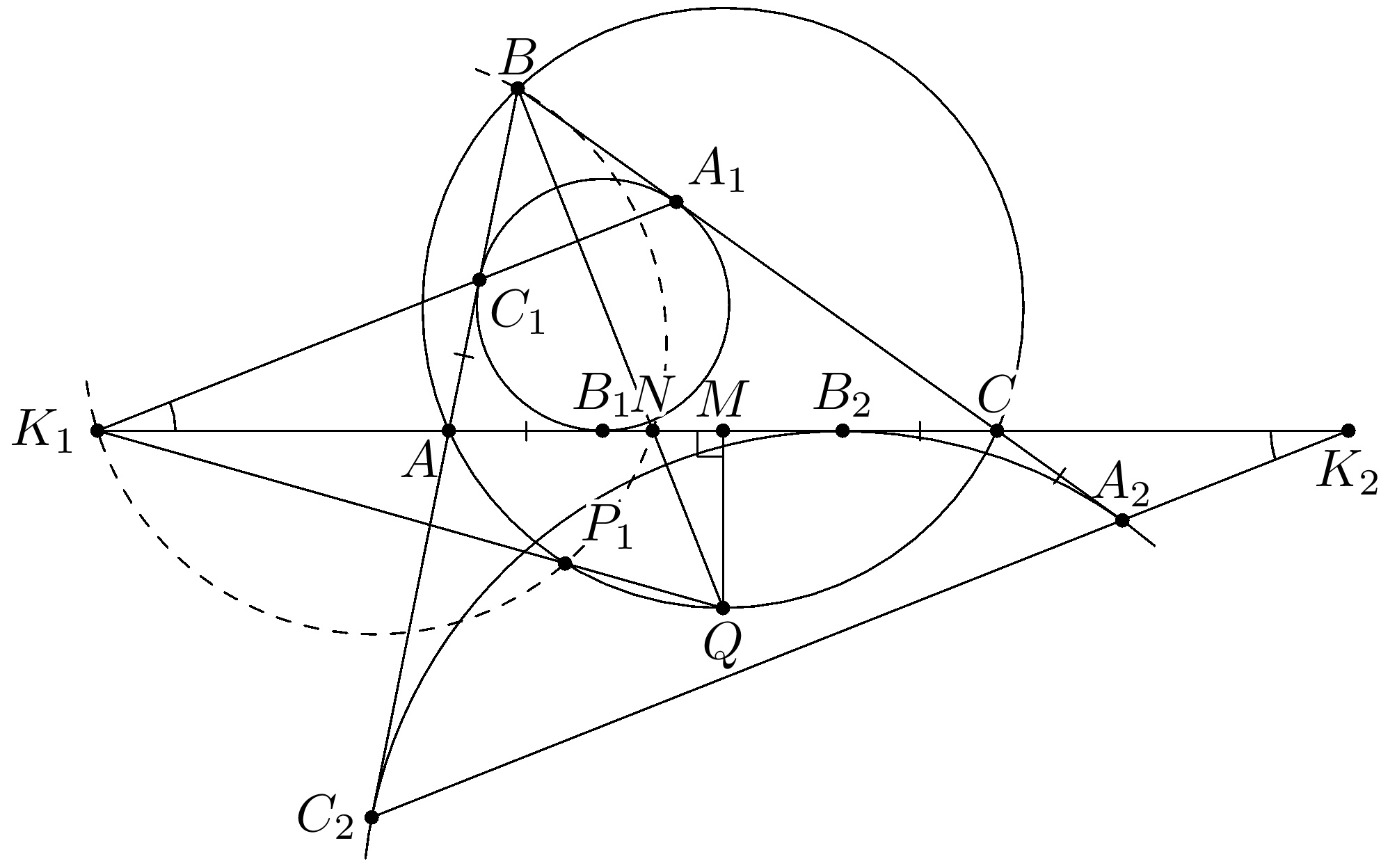
Комментарии от администратора Комментарии от администратора №1.     Не теряя общности положим $BC > AB$. Пусть $M$ — середина $AC$, а $BN$ пересекает описанную окружность треугольника $ABC$ в точке $Q$. Пусть вписанная в вневписанная окружности касаются $AC$ в точках $B_1$ и $B_2$ соответственно.

Известным фактом является то, что $$ AC_1 = AB_1 = CB_2 = CA_2 = (AB+AC-BC)/2. $$ Заметим, что $K_1C_1 \parallel A_2K_2$ и $\angle K_1C_1A + \angle CA_2K_2 = 180^\circ$. Применив теорему синусов для $\triangle K_1C_1A$ и $\triangle CA_2K_2$ получим \[A{K_1} = \sin \angle {K_1}{C_1}A \cdot \frac{{A{C_1}}}{{\sin \angle {C_1}{K_1}A}} = \sin \angle C{A_2}{K_2} \cdot \frac{{C{A_2}}}{{\sin C{K_2}{A_2}}} = C{K_2}.\] Также заметим, что точки $Q$, $P_1$ и $K_1$ лежат на одной прямой, так как \[\angle {K_1}{P_1}B + \angle B{P_1}Q = \angle {K_1}NB + \angle BAQ = \angle C + \angle B/2 + \angle A + \angle B/2 = {180^\circ }.\] Аналогично, точки $Q$, $P_2$ и $K_2$ лежат на одной прямой. Значит, $K_1QK_2$ — равнобедренный треугольник. Поэтому $QP_1 \cdot QK_1 = QN \cdot QB = QP_2 \cdot QK_2$, откуда $QP_1 = QP_2$. Из последнего равенства следует утверждение задачи.