Математикадан облыстық олимпиада, 2015-2016 оқу жылы, 10 сынып

$ABC$ ұшбұрышында $AB$ және $AC$ қабырғалары тең. $A$ төбесінен жүргізілген түзу, $ABC$ үшбұрышына сырттай сызылған шеңберді екінші рет $Z$ нүктесінде, ал центрі $A$ нүктесі және радиусы $AB$ болатын шеңберді — $X$ және $Y$ нүктелерінде қияды. $BX$ және $CY$ түзулері $P$ нүктесінде қиылысады. $CX$, $BY$ және $PZ$ түзулері бір нүктеде қиылысатынын дәлелдеңіз.

Комментарий/решение

Решение. (Рисунок) Т.к. $XY$ – диаметр, $BX⊥BY$ и $CX⊥CY$. Нужно доказать, что $PZ⊥XY$, т.к. тогда $BY,CX,PZ$ будут высотами $\Delta XYP$. Сделаем по-другому: проведем перпендикуляр $PZ'⊥XY$ и докажем, что $Z',A,B,C$ лежат на одной окружности. Это верно, т.к. окружность девяти точек $\Delta XYP$ в точности проходит через середину $A$ и основания высот $B,C,Z'$.

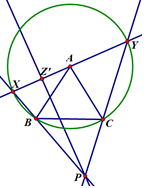
Пересечения $CB$ и $XY$, $BP$ и $YZ$, $PC$ и $ZX$ все лежат на одной прямой $X-Y-Z$

По теореме Дезарга для $\triangle CBP$ и $\triangle XYZ$, прямые $CX, BY, PZ$ пересекаются в одной точке.

Только вот есть вопрос, верно ли мое решение, ведь я даже не использовал равнобедренность?