8-я Жаутыковская олимпиада (2012), теоретический тур
Приключения поршня (10 баллов)
2.1 [0.5 балла] Чему равно давление воздуха $p_1$ в сосуде в конце первой стадии? Ответ выразите через атмосферное давление $p_0$, показатель адиабаты $\gamma$ и параметр $\alpha=Mg/p_0S$. Найдите численное значение $p_1$.
2.2 [1.5 балла] Чему равна температура воздуха $T_1$ в конце первой стадии? Ответ выразите через $T_0$, $\gamma$ и $\alpha=Mg/p_0S$. Найдите численное значение $T_1$.
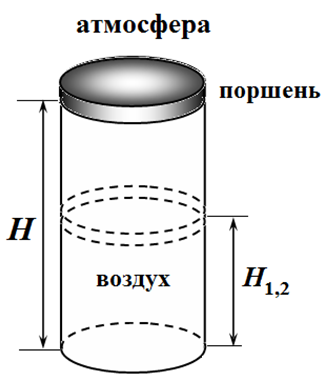
2.3 [0.5 балла] Найдите высоту $H_1$. Ответ выразите через $H$, $\gamma$ и $\alpha=Mg/p_0S$. Найдите численное значение $H_1$.
2.4 [0.5 балла] Чему равно давление воздуха $p_2$ в сосуде в конце второй стадии? Ответ выразите через $p_0$ и $\alpha=Mg/p_0S$. Найдите численное значение $p_2$.
2.5 [0.5 балла] Чему равна температура воздуха $T_2$ в конце второй стадии?
2.6 [0.5 балла] Найдите высоту $H_2$. Ответ выразите через $H$ и $\alpha=Mg/p_0S$. Найдите численное значение $H_2$.
2.7 [2 балла] Найдите частоту $\omega$ малых колебаний поршня около положения равновесия $H_2$, считая процесс квазистатическим и адиабатическим. Ответ выразите через $g$, $H$, $\gamma$ и $\alpha=Mg/p_0S$. Найдите численное значение $\omega$. По окончании второй стадии в дне сосуда проделали множество отверстий суммарной площадью $S_{O}=5\times 10^{-4}$ см$^2$, при этом размер каждого отверстия много меньше длины свободного пробега молекул. Спустя некоторое время поршень начинает двигаться с некоторой постоянной скоростью $u$.
Известно, что среднее число молекул $\overline{N}$, попадающих на единицу площади поверхности в единицу времени равно $$\overline{N}=\frac{1}{4}n\overline{\vartheta},\quad (1)$$ где $\overline{\vartheta}=\sqrt{8RT/\pi\mu}$ — так называемая средняя тепловая скорость молекул, а $n$ — их концентрация. Средняя кинетическая энергия поступательного движения молекул, попадающих в отверстия, равна $$\overline{W}=2k_{B}T, \quad (2)$$ где $k_{B}$ — постоянная Больцмана. Считая поток тепла через стенки и поршень пренебрежимо малым, ответьте на сле-дующие вопросы:
2.8 [1 балл] Установившееся давление воздуха под поршнем имеет вид $p_3=Af(\alpha)$, где $A$ — некоторая постоянная, зависящая от $p_0$, а $f(\alpha)$ — некоторая функция от $\alpha$. Найдите $A$ и $f(\alpha)$. Найдите численное значение $p_3$.
2.9 [2 балла] Установившаяся скорость поршня имеет вид $u=Bg(\alpha)$, где $B$ — некоторая постоянная, зависящая от $S_0$, $S$, $R$, $T_0$ и $\mu$, а $g(\alpha)$ — некоторая функция от $\alpha$. Найдите $B$ и $g(\alpha)$. Найдите численное значение $u$.
2.10 [1 балл] Установившаяся температура газа под поршнем имеет вид $T_3=Ch(\alpha)$, где $C$ — некоторая постоянная, зависящая от $T_0$, а $h(\alpha)$ — некоторая функция от $\alpha$. Найдите $C$ и $h(\alpha)$. Найдите численное значение $T_3$.
посмотреть в олимпиаде
2.1 [0.5 балла] Чему равно давление воздуха $p_1$ в сосуде в конце первой стадии? Ответ выразите через атмосферное давление $p_0$, показатель адиабаты $\gamma$ и параметр $\alpha=Mg/p_0S$. Найдите численное значение $p_1$.
2.2 [1.5 балла] Чему равна температура воздуха $T_1$ в конце первой стадии? Ответ выразите через $T_0$, $\gamma$ и $\alpha=Mg/p_0S$. Найдите численное значение $T_1$.
2.3 [0.5 балла] Найдите высоту $H_1$. Ответ выразите через $H$, $\gamma$ и $\alpha=Mg/p_0S$. Найдите численное значение $H_1$.
2.4 [0.5 балла] Чему равно давление воздуха $p_2$ в сосуде в конце второй стадии? Ответ выразите через $p_0$ и $\alpha=Mg/p_0S$. Найдите численное значение $p_2$.
2.5 [0.5 балла] Чему равна температура воздуха $T_2$ в конце второй стадии?
2.6 [0.5 балла] Найдите высоту $H_2$. Ответ выразите через $H$ и $\alpha=Mg/p_0S$. Найдите численное значение $H_2$.
2.7 [2 балла] Найдите частоту $\omega$ малых колебаний поршня около положения равновесия $H_2$, считая процесс квазистатическим и адиабатическим. Ответ выразите через $g$, $H$, $\gamma$ и $\alpha=Mg/p_0S$. Найдите численное значение $\omega$. По окончании второй стадии в дне сосуда проделали множество отверстий суммарной площадью $S_{O}=5\times 10^{-4}$ см$^2$, при этом размер каждого отверстия много меньше длины свободного пробега молекул. Спустя некоторое время поршень начинает двигаться с некоторой постоянной скоростью $u$.
Известно, что среднее число молекул $\overline{N}$, попадающих на единицу площади поверхности в единицу времени равно $$\overline{N}=\frac{1}{4}n\overline{\vartheta},\quad (1)$$ где $\overline{\vartheta}=\sqrt{8RT/\pi\mu}$ — так называемая средняя тепловая скорость молекул, а $n$ — их концентрация. Средняя кинетическая энергия поступательного движения молекул, попадающих в отверстия, равна $$\overline{W}=2k_{B}T, \quad (2)$$ где $k_{B}$ — постоянная Больцмана. Считая поток тепла через стенки и поршень пренебрежимо малым, ответьте на сле-дующие вопросы:
2.8 [1 балл] Установившееся давление воздуха под поршнем имеет вид $p_3=Af(\alpha)$, где $A$ — некоторая постоянная, зависящая от $p_0$, а $f(\alpha)$ — некоторая функция от $\alpha$. Найдите $A$ и $f(\alpha)$. Найдите численное значение $p_3$.
2.9 [2 балла] Установившаяся скорость поршня имеет вид $u=Bg(\alpha)$, где $B$ — некоторая постоянная, зависящая от $S_0$, $S$, $R$, $T_0$ и $\mu$, а $g(\alpha)$ — некоторая функция от $\alpha$. Найдите $B$ и $g(\alpha)$. Найдите численное значение $u$.
2.10 [1 балл] Установившаяся температура газа под поршнем имеет вид $T_3=Ch(\alpha)$, где $C$ — некоторая постоянная, зависящая от $T_0$, а $h(\alpha)$ — некоторая функция от $\alpha$. Найдите $C$ и $h(\alpha)$. Найдите численное значение $T_3$.
Комментарий/решение:
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.