Temirlan Baibolov

Задача №1.

Задача B. Друзья

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

В HS учатся $n$ студентов включая Руслана. Для удобства пронумеруем всех студентов целыми числами от $1$ до $n$, а у Руслана всегда номер $1$. Известно, что среди студентов есть ровно $m$ пар друзей $(a_1, b_1), \ldots, (a_m, b_m)$. Пара $(a_i, b_i)$ означает что студенты под номерами $a_i$ и $b_i$ являются друзьями. Недавно Руслан открыл свой кружок по спортивному программированию. Теперь ему нужно пригласить туда как можно больше студентов. По вполне логичным причинам, Руслан сперва начнет приглашать своих друзей. Затем его друзья смогут пригласить своих друзей, а они — своих друзей и так далее. Однако не все так просто! У каждого студента в HS есть свой навык убеждения $c_i$. Также определим навык убеждения кружка как сумму навыков убеждений каждого отдельного члена кружка. Изначально навык убеждения кружка равен навыку убеждения Руслана: значению $c_1$. Нового студента можно пригласить в кружок только тогда, когда навык убеждения кружка не меньше навыка убеждения этого студента. Более формально, в любой момент времени любой участник кружка может позвать в кружок своего друга, при условии что сумма навыков убеждений всех членов кружка не меньше навыка убеждения этого друга. Разрешено набирать в кружок новых студентов до тех пор, пока это возможно.

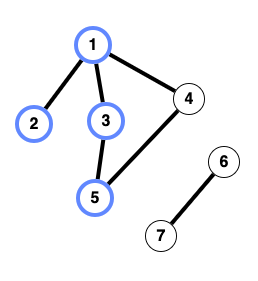
Визуализация первого примера. Синим помечены студенты вступившие в кружок.

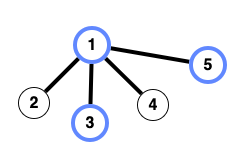
Визуализация второго примера. Синим помечены студенты вступившие в кружок.

Какое максимальное количество студентов Руслан сможет набрать к себе в кружок (включая самого Руслана)?

Формат входного файла

В первой строке входного файла даны два целых числа $n$ и $m$ — количество студентов в HS и количество пар друзей ($2 <= n <= 2 \cdot 10^5$, $0 <= m <= 2 \cdot 10^5$). В следующих $m$ строках содержатся пары $(a_i, b_i)$, обозначающие пары друзей среди студентов. ($1 <= a_i, b_i <= n$, $a_i \neq b_i$) В последней строке содержатся $n$ целых чисел $c_1, \ldots, c_n$ — навыки убеждения каждого из студентов. ($1 <= c_i <= 10^9$) Гарантируется, что никакая пара студентов не встречается в списке друзей дважды.

Формат выходного файла

Выведите одно целое число — максимальное количество студентов которых Руслан сможет набрать к себе в кружок.

Примеры:

Вход

7 6
1 2
3 1
1 4
5 3
4 5
6 7
2 2 1 12 5 3 6

Ответ

Вход

5 4
1 2
1 3
1 4
1 5
4 18 6 16 4

Ответ

Вход

2 0
1 1

Ответ

Замечание

Разберем первый пример.

Изначально Руслан один в секции. Навык убеждения кружка равен $c_1 = 2$. Руслан может пригласить в кружок друзей $2$ и $3$, но не может пригласить друга $4$, поскольку его навык убеждения $c_4 = 12 > 2$.
Теперь в секции Руслана есть студенты $1$, $2$ и $3$. Навык убеждения кружка равен $c_1 + c_2 + c_3 = 2 + 2 + 1 = 5$. Студент номер $3$ может пригласить своего друга $5$ ($c_5 = 5 <= 5$). По прежнему пригласить студента $4$ не удается ($c_4 = 12 > 5$).
Теперь в секции Руслана есть студенты $1$, $2$, $3$ и $5$. Навык убеждения кружка равен $c_1 + c_2 + c_3 + c_5 = 2 + 2 + 1 + 5 = 10$. Однако больше никаких студентов позвать в кружок невозможно. Студенты $6$ и $7$ не являются друзьями студентов в секции, а у студента $4$ по прежнему навык убеждения больше ($c_4 = 12 > 10$).

( Temirlan Baibolov )
комментарий/решение олимпиада

Задача №2.

Задача A. Башни

Ограничение по времени:

1.5 секунд

Ограничение по памяти:

256 мегабайт

В одном ряду последовательно расположили $n$ башен из кубиков. $i$-я башня состоит из $a_i$ кубиков, которые выставлены вертикально друг над другом. Гарантируется, что все башни состоят из не более чем $k$ кубиков. Все кубики подчиняются закону гравитации — они падают вниз до тех пор пока не коснутся пола или верхней стороны другого кубика. А также в задаче есть слои льда. Если на высоте $y$ есть лед, это означает что никакой кубик не может упасть с высоты $y+1$ на $y$ пока этот лед не исчезнет. BThero последовательно дает вам $q$ запросов трех видов.

Вам дается одно единственное число $y$, и на высоте $y$ появляется слой льда.
Вам дается одно единственное число $y$, и на высоте $y$ исчезает слой льда.
Вам дается одно единственное число $y$, и на высоте $y$ устанавливается новый лазер. Гарантируется, что на этой высоте ранее еще не был установлен никакой лазер. Номером этого лазера будет являться минимальное еще не занятое положительное число. Лазер можно представить как бесконечную горизонтальную линию на высоте $y$ и он будет уничтожать все кубики и слои льда которые его касаются. Может быть такое, что лазер уничтожил кубик, а сверху по закону гравитации на его место упал другой кубик. Тогда тот кубик тоже уничтожится, и процесс может повториться снова.

Обозначим суммарное количество установленных лазеров как $m$. После всех запросов выведите количество уничтоженных кубиков для каждого лазера.

Формат входного файла

В первой строке входного файла даны три целых числа $n$, $q$ и $k$ — количество башен, количество запросов и ограничение на количество кубиков в башнях ($1 <= n, q <= 300000$, $1 <= k <= 10^9$). Во второй строке даны $n$ целых чисел $a_1$, \dots, $a_n$ ($1 <= a_i <= k$). В последующих $q$ строках даны все запросы в формате $t_i$, $y_i$ — тип $i$-го запроса и число, связанное с этим запросом ($1 <= t_i <= 3$, $1 <= y_i <= k$).

Формат выходного файла

Выведите $m$ целых чисел $c_1$, \dots, $c_m$ разделенные пробелами — количество уничтоженных клеток для каждого лазера. Гарантируется, что $m > 0$.

Система оценки

Данная задача содержит $7$ подзадач.

Примеры из условия. Оценивается в $0$ баллов.
$n, k, q <= 100$. Оценивается в $15$ баллов.
$n, k, q <= 5000$, $t_i = 3$ для всех $1 <= i <= q$. Оценивается в $8$ баллов.
$n, k, q <= 5000$. Оценивается в $13$ баллов.
$k <= 300000$. Оценивается в $19$ баллов.
$t_i \neq 2$ для всех $1 <= i <= q$. Оценивается в $16$ баллов.
Исходные условия задачи. Оценивается в $29$ баллов.

Пример:

Вход

Ответ

10 4 4

( Temirlan Baibolov )
комментарий/решение олимпиада

Задача №3.

Задача A. Покраска суммой

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

У вас есть массив целых чисел $a_1, \ldots, a_n$ размера $n$. Изначально каждое число массива покрашено в белый цвет. За одну операцию вы можете:

Выбрать три белых числа $(a_i, a_j, a_k)$ ($1 <= i, j, k <= n$, $i \neq j$, $i \neq k$, $j \neq k$).
Если значение $a_i + a_j$ строго больше $a_k$, покрасить $a_k$ в черный цвет.

Вы обязаны повторять эту операцию до тех пор, пока это возможно. В процессе некоторые числа будут перекрашены в черный цвет, а остальные — останутся белыми. От вас требуется посчитать количество всевозможных конечных раскрасок.

Формат входного файла

В первой строке входного файла дано одно целое число $n$ — размер массива ($3 <= n <= 10^5$). Во второй строке даны $n$ целых чисел $a_1, \ldots, a_n$ ($-10^9 <= a_i <= 10^9$).

Формат выходного файла

Выведите одно целое число — количество всевозможных конечных раскрасок. Можно показать, что в заданных ограничениях ответ никогда не превосходит $10^{18}$.

Примеры:

Вход

3
2 2 5

Ответ

Вход

4
-3 1 2 2

Ответ

( Temirlan Baibolov )
комментарий/решение(2) олимпиада

Задача №4.

Задача E. Шоколадки

Ограничение по времени:

2.5 секунд

Ограничение по памяти:

256 мегабайт

Айбар и Данияр решили купить шоколадки перед олимпиадой. Допустим, в магазине продаются $n$ видов шоколадок пронумерованных от $1$ до $n$. У каждого вида шоколадки $i$ есть свой уровень сладости $a_i$. Айбар и Данияр договорились покупать шоколадки по следующей нехитрой схеме:

Сперва Айбар купит шоколадку с самой большой сладостью. Затем Данияр тоже купит шоколадку с самой большой сладостью среди других видов шоколадок. Более формально, если Айбар купил шоколадку вида $i$, Данияр должен купить шоколадку вида $j \neq i$ такую, что её сладость самая большая.
Теперь Айбар купит шоколадку с самой маленькой сладостью. Затем Данияр тоже купит шоколадку с самой маленькой сладостью среди других видов шоколадок. Более формально, если Айбар купил шоколадку вида $i$, Данияр должен купить шоколадку вида $j \neq i$ такую, что её сладость самая маленькая.

В конце Айбар и Данияр суммируют сладости купленных ими шоколадок. Если их посчитанные суммы оказываются одинаковыми, то побеждает дружба. Например, если бы в магазине продавали $n = 4$ видов шоколадок со сладостями $[1, 4, 6, 3]$, то Айбар бы купил шоколадки вида $3$ и $1$ с суммарной сладостью $6 + 1 = 7$. А Данияр бы купил шоколадки вида $2$ и $4$ с суммарной сладостью $4 + 3 = 7$ и в конце победила бы дружба. В этой задаче можно считать что есть не менее двух шоколадок каждого вида. Если бы в магазине было всего лишь $n = 2$ видов шоколадок, они оба купили бы по одной шоколадке вида $1$ и $2$. Друзья решили не мелочиться и сразу зайти в супермаркет. В супермаркете продаются $n$ видов шоколадок со сладостями $b_1, \ldots, b_n$. Теперь друзьям стало интересно, сколько есть пар $1 <= i < j <= n$ таких, что если друзья будут покупать шоколадки только среди видов $(i, \ldots, j)$ победит дружба?

Формат входного файла

В первой строке дано одно целое число $n$ — количество видов шоколадок в супермаркете ($2 <= n <= 250000$). Во второй строке даны $n$ чисел $b_1, \ldots, b_n$ ($1 <= b_i <= 10^9$).

Формат выходного файла

Выведите одно целое число — количество искомых пар.

Примеры:

Вход

3
1 2 3

Ответ

Вход

5
1 1 3 2 1

Ответ

Замечание

Во втором примере, подходят следующие пары: $(1, 2), (2, 3), (2, 4), (3, 4), (3, 5), (4, 5)$ ( Temirlan Baibolov )
комментарий/решение олимпиада

Задача №5.

Задача D. Сумма-делимые отрезки

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

Вам даны два массива положительных целых чисел $a$ и $b$ длины $n$. Нумерация обоих массивов начинается с $1$. Посчитайте количество отрезков $(l, r)$ таких, что $1 <= l <= r <= n$ и $a_l + \ldots + a_r$ нацело делится на $b_l + \ldots + b_r$. Простыми словами, сумма массива $a$ на этом отрезке должна делиться без остатка на сумму массива $b$ на том же отрезке.

Формат входного файла

В первой строке дано одно целое число $n$ — длины массивов ($1 <= n <= 10^5$). Во второй строке даны числа $a_1$, \ldots, $a_n$ ($1 <= a_i <= 10$). В третьей строке даны числа $b_1$, \ldots, $b_n$ ($1 <= b_i <= 10$).

Формат выходного файла

Выведите одно целое число — количество подходящих отрезков $(l, r)$.

Система оценки

Данная задача состоит из $10$ тестов. Каждый тест оценивается в $10$ баллов.

[(1-2)] Примеры из условия.
[(3-4)] $n = 1$.
[(5-6)] $n = 100$.
[(7-8)] $n = 2000$.
[(9-10)] $n = 100000$.

Примеры:

Вход

3
1 2 3
1 1 1

Ответ

Вход

5
2 3 1 5 4
3 2 2 1 2

Ответ

Замечание

В первом примере подходят $4$ отрезка $(1, 1)$, $(2, 2)$, $(3, 3)$, $(1, 3)$. Отрезок $(1, 3)$ подходит, потому что $a_1+a_2+a_3=1+2+3=6$ делится без остатка на $b_1+b_2+b_3=1+1+1=3$. ( Temirlan Baibolov )
комментарий/решение(1) олимпиада

Задача №6.

Задача D. Две очереди

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

Есть две очереди. В первой стоят $n$ людей, во второй стоят $m$ людей. В первой очереди обслуживают одного человека за $A$ минут, во второй очереди обслуживают одного человека за $B$ минут. Отсчет времени начинается с минуты $1$. Каждую минуту последовательно происходит следующее:

Если первый человек в первой очереди обслужен, то он уходит из очереди.
Если первый человек во второй очереди обслужен, то он уходит из очереди.
Последний человек в первой очереди перемещается в конец второй очереди если его порядковый номер во второй очереди окажется меньше чем его номер в первой очереди.
Последний человек во второй очереди перемещается в конец первой очереди если его порядковый номер в первой очереди окажется меньше чем его номер во второй очереди.

Сообщите первый момент времени $T$ когда все люди будут обслужены.

Формат входного файла

В первой и единственной строке входного файла даны четыре целых числа $n$, $m$, $A$ и $B$ ($1 <= n, m, A, B <= 10^5$).

Формат выходного файла

Выведите одно целое число — первый момент времени $T$ когда все люди будут обслужены.

Примеры:

Вход

2 3 1 2

Ответ

Вход

5 6 4 4

Ответ

Вход

3 1 2 4

Ответ

Замечание

Разберем первый пример. Минута $1$. Первый человек из первой очереди обслужен и уходит из очереди. Теперь $n=1$, $m=3$. Последний человек во второй очереди переходит в конец первой очереди. Теперь $n=2$, $m=2$. Минута $2$. Первый человек из первой очереди обслужен и уходит из очереди. Теперь $n=1$, $m=2$. Первый человек из второй очереди обслужен и уходит из очереди. Теперь $n=1$, $m=1$. Больше ничего не происходит. Минута $3$. Первый человек из первой очереди обслужен и уходит из очереди. Теперь $n=0$, $m=1$. Больше ничего не происходит. Минута $4$. Первый человек из второй очереди обслужен и уходит из очереди. Теперь $n=0$, $m=0$. Все люди обслужены, значит ответ $T=4$. ( Temirlan Baibolov )
комментарий/решение олимпиада

Задача №7.

Задача B. Игра-платформер

Ограничение по времени:

2 секунды

Ограничение по памяти:

256 мегабайт

Нархан недавно создал свою оригинальную игру-платформер. Как в большинстве игр похожего жанра, всё действие игры происходит в двумерном пространстве. Весь мир игры можно описать как один большой прямоугольник, соединяющий точки $(0, 0)$ и $(m, 10^9)$. Все объекты в игре находятся внутри этого прямоугольника. Прямая $y=0$ считается землей. В игре действует обычная гравитация. Игрок начинает игру в точке $(0, 0)$ и для победы нужно добраться до точки $(m, 0)$. В игре также присутствуют $n$ препятствий. Каждое препятствие также можно описать как прямоугольник. Все препятствия лежат на земле, т.е. напрямую касаются земли. Расположение каждого из них описывается тремя целыми числами $L_i$, $R_i$ и $H_i$ — $x$-координатой левого конца прямоугольника, $x$-координатой правого конца прямоугольника и высотой прямоугольника. Препятствия не пересекаются между собой, но могут касаться друг-друга. Также гарантируется, что никакое препятствие не содержит начальную точку $(0, 0)$ и конечную точку $(m, 0)$. Игрок может свободно перемещаться налево или направо. Однако игрок не может проходить сквозь препятствия или обходить их. Но игрок может подниматься и опускаться по сторонам препятствий. На каждое перемещение игрока тратится ровно одна секунда. Нархан попросил Аманбола пройти эту игру. Аманбол очень ленивый, поэтому он не хочет тратить большое количество времени на прохождение игры. Поэтому перед началом игры он может попросить Нархана передвинуть некоторые препятствия. Он может выбрать произвольное препятствие $i$ ($1 <= i <= n$) и попросить Нархана подвинуть это препятствие на одну единицу налево или на одну единицу направо при условии что все правила игры всё еще выполняются (препятствия не должны пересекаться и не должны содержать начальную или конечную точку). Нархану потребуется ровно $C_i$ секунд чтобы выполнить просьбу Аманбола. Аманбол может просить Нархана подвинуть прямоугольники неограниченное (возможно $0$) количество раз. За какое минимальное суммарное время он сможет пройти игру?

Формат входного файла

В первой строке входного файла содержатся два целых числа $n$ и $m$ — количество препятствий и координата конечной точки ($1 <= n <= 5 \cdot 10^5$, $1 <= m <= 3 \cdot 10^6$). В $i$-й из последующих $n$ строк содержатся четыре целых числа $L_i$, $R_i$, $H_i$ и $C_i$ — координата левого конца, координата правого конца, высота и стоимость передвижения $i$-го препятствия ($1 <= L_i < R_i <= m-1$, $1 <= H_i <= 10^9$, $0 <= C_i <= 3 \cdot 10^6$, $R_i <= L_{i+1}$ для всех $i$).

Формат выходного файла

Выведите одно единственное целое число — минимальное суммарное количество секунд, необходимое Аманболу для прохождения игры.

Система оценки

Данная задача содержит $6$ подзадач.

Примеры:

Вход

Ответ

Вход

Ответ

Замечание

Разберем первый пример.

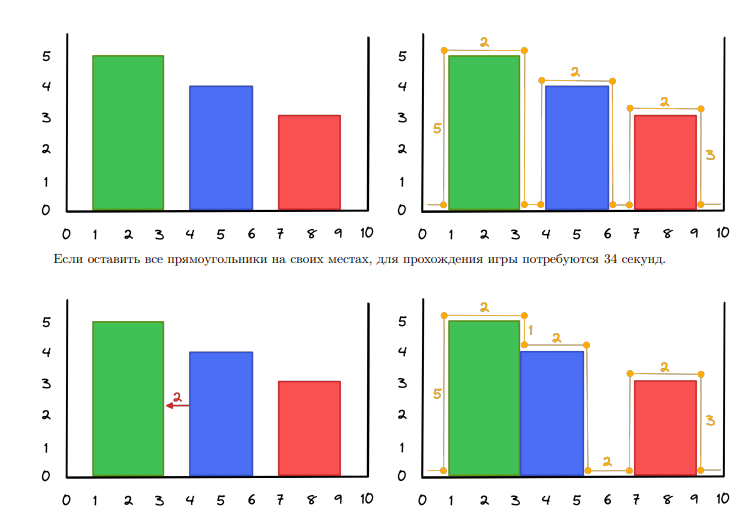Но Аманбол может попросить подвинуть второй прямоугольник на единицу налево за $2$ секунды. Теперь для прохождения игры потребуются $26$ секунд. В итоге получилось $28$ секунд.

( Temirlan Baibolov )
комментарий/решение олимпиада