XIII математическая олимпиада «Шелковый путь», 2014 год

Касательные в точках $A$ и $B$ к окружности $\omega$, описанной около остроугольного неравнобедренного треугольника $ABC$, пересекаются в точке $S$. Пусть $M$ — середина стороны $AB$, а $H$ — точка пересечения высот треугольника $ABC$. Прямая $HA$ пересекает прямые $CM$ и $CS$ в точках $M_a$ и $S_a$ соответственно. Аналогично определены точки $M_b$ и $S_b$. Докажите, что $M_a S_b$ и $M_b S_a$ — высоты треугольника $M_a M_b H$. ( М. Кунгожин )

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Пусть $AC>CB$, и $AA_1$, $BB_1$ — высоты треугольника $ABC$. Известным фактом является то, что $\angle ACM = \angle SCB$ (это факт известен как свойство симедианы). Так как $\angle HAC = \angle HBC$, то $$\angle S_aM_aM_b = \angle HAC + \angle ACM = \angle HBC + \angle SCB = \angle M_bS_bC,$$ то есть точки $M_a$, $M_b$, $S_a$, $S_b$ лежат на одной окружности. Докажем, что $M_aS_b \perp HM_b$. Проведем перпендикуляр $\ell$ к прямой $CM$ в точке $C$. Пусть $AA_1 \cap \ell = A_2$, $BB_1 \cap \ell = B_2$, а $X$ и $Y$ — точки на прямой $\ell$ такие, что $AX \parallel CM \parallel BY$. Тогда $CX=CY$. Имеем: $$CX \cdot CB_2 = CB_1 \cdot CA = CA_1 \cdot CB = CY \cdot CA_2,$$ откуда $CB_2 = CA_2$, то есть прямая $CM$ лежит на серединном перпендикуляре отрезка $A_2B_2$. Следовательно, $\angle M_bS_bC = \angle S_aM_aM_b = CM_aB_2$, откуда точки $B_2$, $C$, $S_b$, $M_a$ также лежат на одной окружности. Значит, $\angle M_aS_bB_2 = M_aCB_2=90^\circ$. Перпендикулярность прямых $M_bS_a$ и $HM_a$ доказывается аналогично.

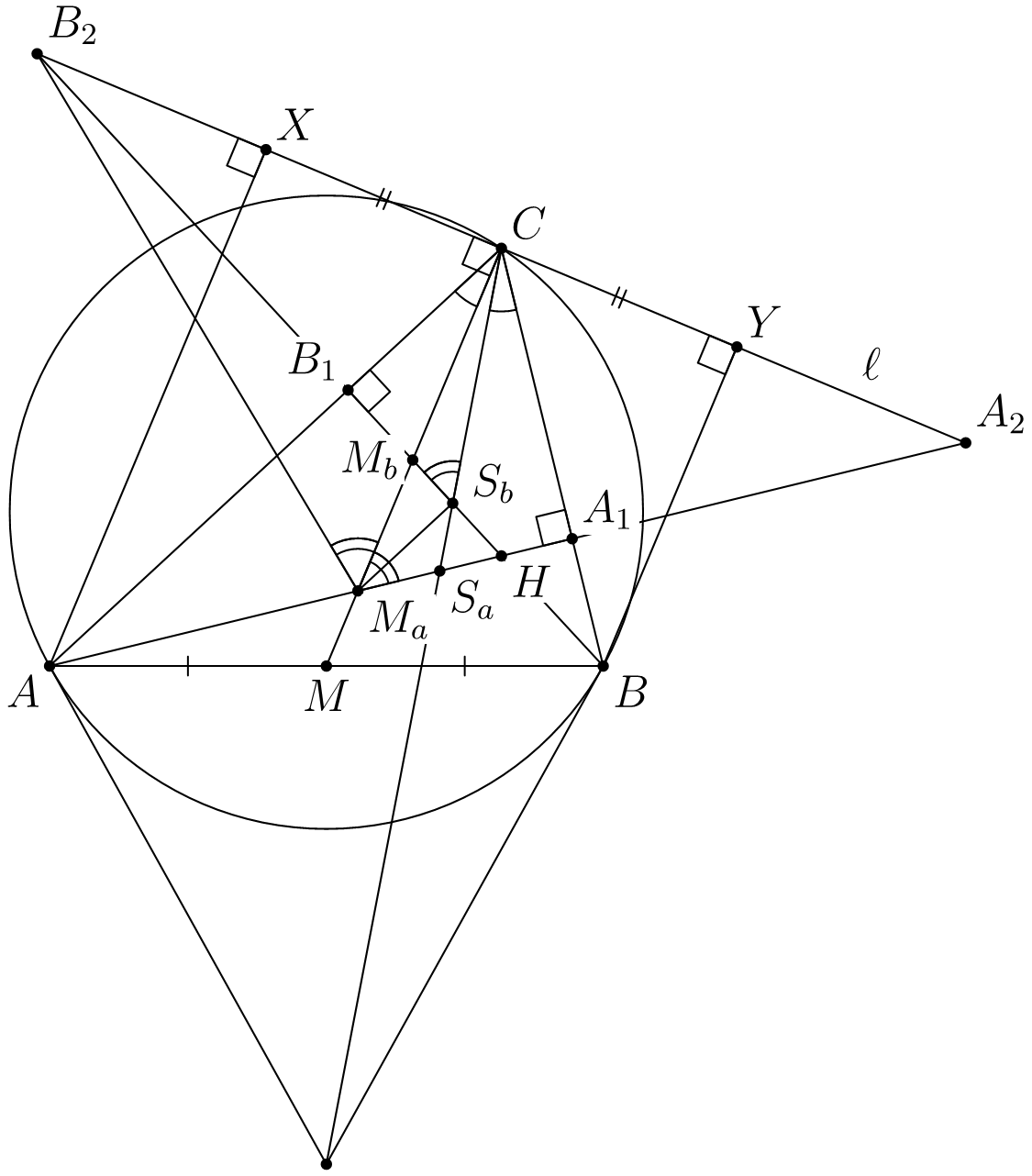
Без ограничения общности примем, что $AC<BC$.

Пусть основания высот в $\triangle ABC$ из точке $A,B$ соответственно $A_1, B_1$

Примем обозначения $:$

$AC=b, BC=a,\angle BAC=\alpha, \angle ABC=\beta, \angle ACB=\gamma, \angle BCM=x, \angle ACM=y.$

Так как $CM-$медиана, то $\dfrac{\sin x}{\sin y}=\dfrac{b}{a}$

Заметим, что $CS-$ симедиана,

откуда $\angle ACS=\angle BCM=x$ и $\angle BCS=\angle ACM=y.$

Докажем, что $S_aM_b\parallel BC\iff \dfrac{HA_1}{HB}=\dfrac{S_aA_1}{M_bB}$,

но $\dfrac{HA_1}{HB}=\cos BHA_1=\cos \gamma.$

Тогда достаточно доказать, что $\dfrac{S_aA_1}{M_bB}=\cos \gamma.$

Заметим, что $CA_1=b\cos\gamma, CB_1=a\cos\gamma, AA_1=b\sin\gamma, BB_1=a\sin\gamma.$

Отметим, что $CS_a=\dfrac{CA_1}{\cos\angle BCS_a}=\dfrac{b\cos\gamma}{\cos y}$

Так же $CM_b=\dfrac{CB_1}{\cos\angle B_1CM_b}=\dfrac{a\cos\gamma}{\cos y}$

Заметим, что в $\triangle S_aCA_1:$ $S_aA_1=CS_a \sin y$

По т. Синусов в $\triangle M_bBC: M_bB=\dfrac{CM_b}{\sin{\angle CBM_b}}\cdot \sin x=\dfrac{CM_b}{\cos\gamma}\cdot \sin x$

Тогда $$\dfrac{S_aA_1}{M_bB}=\dfrac{CS_a \sin y}{\dfrac{CM_b}{\cos\gamma}\cdot \sin x}=\dfrac{CS_a}{CM_b}\cdot\dfrac{\sin y}{\sin x}\cdot \cos\gamma=\dfrac{b}{a}\cdot\dfrac{\sin y}{\sin x}\cdot\cos\gamma=\cos\gamma$$

откуда $S_aM_b\parallel BC\implies S_aM_b\bot HM_a$, так как $BC\bot HM_a$.

Аналогично $S_bM_a\bot HM_b$.

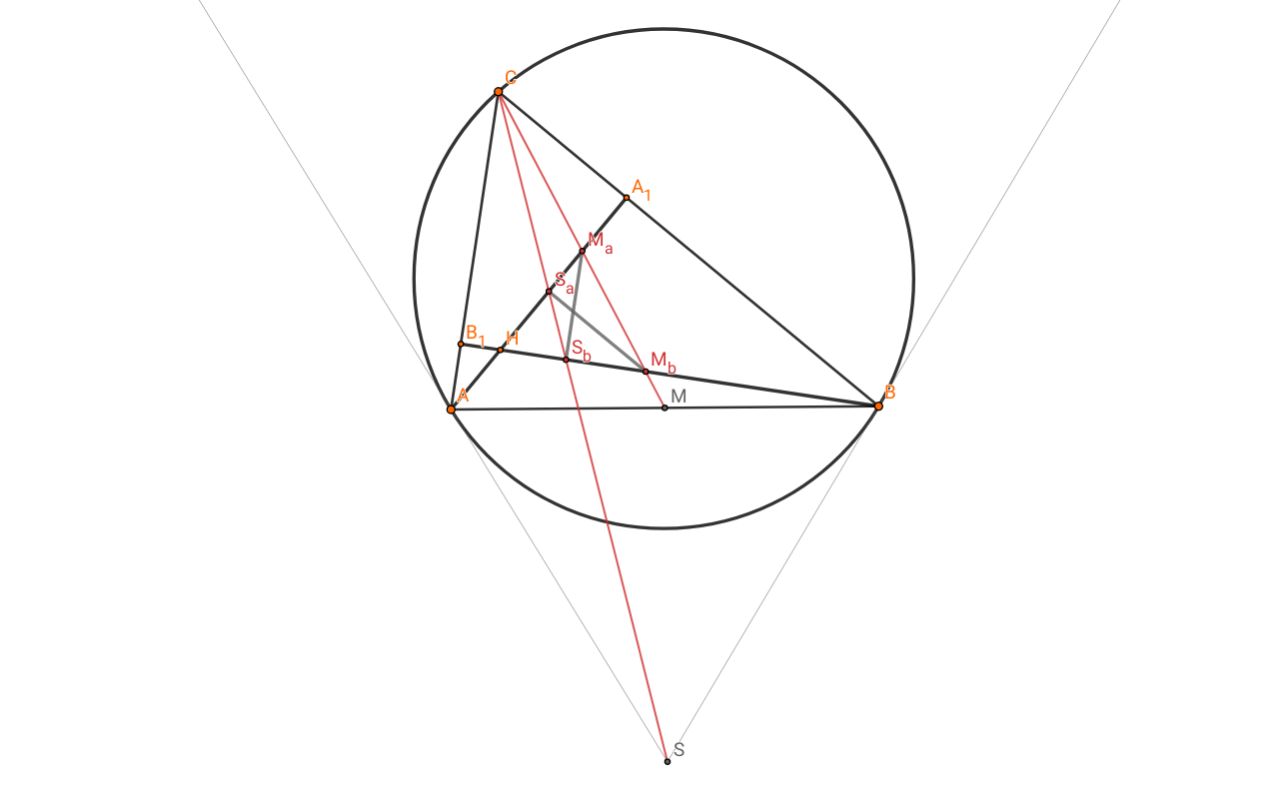
$A_1B_1 \cap AB=T$ и проведем высоту $C_1$ . Переформулируем условие и докажем что $CS_bS_a$ симедиана. Очевидно что $TH$ перпендикулярно медиане в точке F.Заметим что

$$-1=(T,C_1;B,A)\overset{H}{=}(F,C;M_b,M_a)$$ отсюда очевидно что $C-S_a-S_b$ колинеарны.

И так как $A_1S_aC=\angle CM_bB_1$ значит $\angle A_1CS_a=\angle MCB_1$ отсюда $CS_bS_a$ симедиана.