Математикадан аудандық олимпиада, 2014-2015 оқу жылы, 9 сынып

$ABC$ үшбұрышында $B$ төбесінің ішкі биссектрисасы мен $C$ төбесінің сыртқы биссектрисасы $D$ нүктесінде қиылысады. $ABC$ үшбұрышына сырттай сызылған шеңбер $BD$ түзуін екінші рет $E$ нүктесінде қияды. $E$ — $ACD$ үшбұрышына сырттай сызылған шеңбердің центрі екенін дәлелдеңіз.

Комментарий/решение

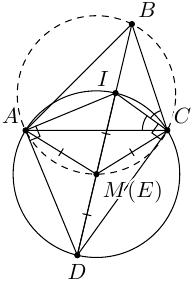
Комментарии от администратора Комментарии от администратора №1.     Решение. Известно, что в треугольнике внутренняя биссектриса одного угла и внешние биссектрисы двух других, пересекаются в одной точке. Также известно, что биссектрисы смежных углов перпендикулярны. Тогда, если $I$ — точка пресечения биссектрис треугольника $ABC$, то $\angle ICD=\angle IAD = 90^\circ$.
Пусть $M$ — середина отрезка $ID$. Из свойств прямоугольного треугольника следуют равенства $MD=MI=MA=MC$, то есть $M$ — центр описанной окружности четырехугольника $AICD$. Тогда, с одной стороны $\angle ICA= \angle IMA/2$, с другой $\angle ICA=\angle ACB/2$, откуда $\angle IMA=\angle ACB$. Следовательно, точка $M$ лежит на описанной окружности треугольника $ABC$, то есть точки $M$ и $E$ совпадают.