Республиканская олимпиада по математике, 2015 год, 10 класс

Даны две окружности $\omega_1$ и $\omega_2$, отрезки $AB$ и $CD$ — общие внешние касательные к ним (точки $A$ и $C$ лежат на $\omega_1$, а точки $B$ и $D$ — на $\omega_2$). Прямая $AD$ во второй раз пересекает окружность $\omega_1$ в точке $P$, а окружность $\omega_2$ в точке — $Q$. Пусть касательная к $\omega_1$ в точке $P$ пересекает $AB$ в точке $R$, а касательная к $\omega_2$ в точке $Q$ пересекает $CD$ в точке $S$. $M$ — середина отрезка $RS$. Докажите, что $MP=MQ$. ( М. Кунгожин )

Комментарий/решение

h_Рисунок@http://my-files.ru/cbnqc8_h

Введем обозначения пусть $O_{1} R_{1},O_{2} , R_{2}$ - центры и радиусы соответственных окружностей и $Y,X$- вторые точки пересечения тех же касательных с прямыми $CD,AB$.

Из условия следует что $AC || BD$ или $ABCD$-равнобедренная трапеция $AB=CD$. Положим что $\angle QO_{2}D=x , \angle AO_{1}P=y$,так как $AC || BD$ получаем что

$\angle PO_{1}C = \angle BO_{2}Q = a = 180-\dfrac{x+y}{2}$. Заметим что $AP=QD$$(1)$ равенство следует из теоремы о секущей и касательной , то есть $AB^2=CD^2=AD(AP+PQ)=AD(QD+PQ)$ откуда $AP=QD$.

Докажем что $AM=MD$ из которой и будет следовать утверждение задачи $MP=MQ$ с учетом факта $(1)$.Опустим перпенидкуляр $l$ из точки $S$ на отрезок $AB$ и $F \in AB \cap l$ , аналогично определим точку $E$ проведенной из вершины $R$.

Тогда получим что точки $E,R,F,S$ лежат на окружности $\omega$ с диаметром $RS$. Заметим что утверждение $MP=MQ$ следует из того что касательные проведенные с вершин $D,A$ к окружности $\omega$ равны. Тогда справедливо равенство

$SD \cdot DE = AR \cdot AF$$(2)$ (из той же теоремы о касательной и секущей),перепишем условие $(2)$ как $(CD-CE)\cdot SD = (CD-BF) \cdot AR$.

Проведем $SO_{2}$ до пересечения с прямой $AB$ пусть $ N \in SO_{2} \cap AB$ , тогда $SN || O_{1}R$ и $\Delta FNS, \Delta BO_{2}N$ подобны , найдем $\angle SXB = \angle CYR = \dfrac{x+y}{2}$

Из подобия следует $\frac{BF+BN}{SO_{2}+NO_{2}} = \frac{BN}{NO_{2}}=sin(\frac{y}{2})$ $(3)$ , но $BN=R_{2}tg(\frac{y}{2})$ так же $NO_{2}=\frac{R_{2}}{cos(\dfrac{y}{2})}$ и $SO_{2} = \frac{R_{2}}{cos(\frac{x}{2})}$ подставляя в $(3)$ получим $BF=\dfrac{R_{2}\cdot sin(\frac{y}{2})}{cos(\frac{x}{2})}$ , аналогично $ CE = \dfrac{ R_{1}sin(\frac{x}{2})}{cos( \frac{y}{2})}$ . Найдя остальные отрезки $ SD= R_{2}tg( \frac{x}{2}) , \ AR= R_{1} tg(\frac{y}{2}) , \ CD=ctg (\frac{y-x}{4}) \cdot (R_{2}-R_{1}) $ в подставляя найденные значения в $(2)$ учитывая то что $ \dfrac{R_{2}}{R_{1}} = \dfrac{ sin( \frac{y}{2})}{sin ( \frac{x}{2})}$ получим тождество , следовательно $\Delta AMD$ - равнобедренный , помня факт $(1)$ $\Delta MAP = \Delta MDQ$ или $MP=MQ$ .

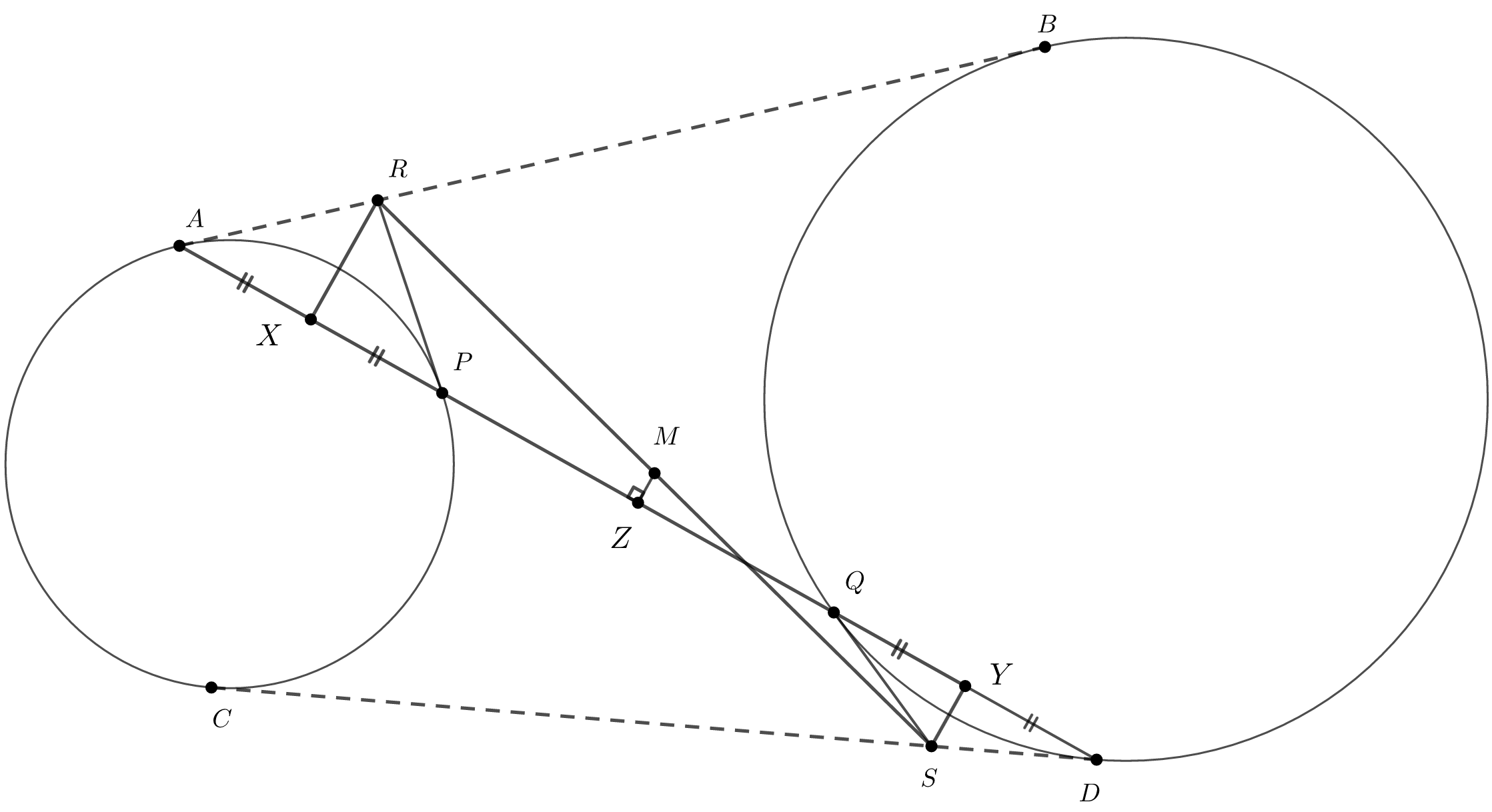
Пусть $X,Y$ середины отрезков $AP,DQ,$ соответственно. Тогда $RX\perp XY\perp SY.$

Из степени точки, получаем $$DP\cdot DA=DC^2=AB^2=AQ\cdot AD\implies DP=AQ\implies PX=QY.$$

Допустим, что $Z$ середина отрезка $XY,$ тогда $RX\parallel SY\parallel MZ,$ поэтому $MZ$ серединный перпендикуляр отрезка $XY,$ откуда $$MX=MY\implies MP=MQ.\quad\square$$