Азиатско-Тихоокеанская математическая олимпиада, 2015 год
Пусть $n$ — натуральное число. Даны $2n$ различных прямых на плоскости, среди которых нет двух параллельных.
Некоторые $n$ из этих $2n$ прямых покрашены синим, а оставшиеся $n$ прямых покрашены красным. Через $\mathcal B$ обозначим множество всех точек
плоскости, принадлежащих хотя бы одной синей прямой, а через
$\mathcal R$ обозначим множество всех точек плоскости, принадлежащих хотя бы одной красной прямой.
Докажите, что существует окружность, которая имеет с множеством $\mathcal B$ ровно $2n-1$ общих точек и
с множеством $\mathcal R$ тоже имеет ровно $2n-1$ общих точек.
(
Pakawut Jiradilok,
Warut Suksompong
)
посмотреть в олимпиаде
Комментарий/решение:
Комментарии от администратора Комментарии от администратора №1. Рассмотрим прямую $\ell$ на плоскости и такую точку $P$ на ней, что $\ell$ не параллельна никакой из $2n$ наших прямых. Будем поворачивать $\ell$ относительно $P$ против часовой стрелки, пока она не станет параллельной одной из $2n$ прямых. Запомним эту прямую и продолжим такие вращения, пока не переберем все прямые. Теперь все наши $2n$ прямых упорядочены по мере того, как они нами выбирались. Обозначим их через $\ell_1$, $\ldots$, $\ell_{2n}$. Ясно, что существуют такие $k \in {\{1, \ldots, 2n - 1\}}$, что $\ell_k$ и $\ell_{k+1}$ разного цвета.
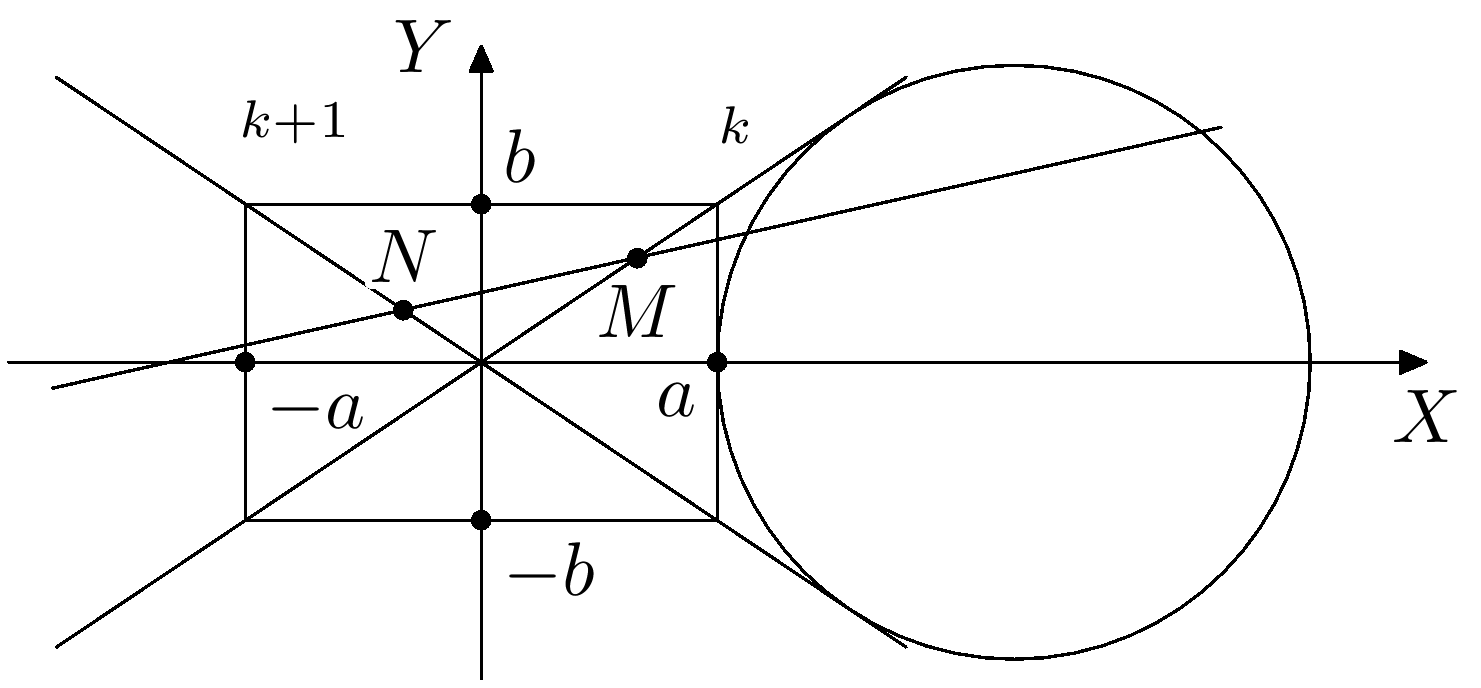
Поскольку все $2n$ прямых различны, множество $S$ всех точек пересечения $\ell_i$ и $\ell_j (i \ne j)$ конечно. Рассмотрим прямоугольник с двумя противоположными вершинами, лежащими на $\ell_k$, и двумя другими вершинами, лежащими на $\ell_{k+1}$. Ясно, что можно увеличивать длины сторон этого прямоугольника до бесконечности. Поэтому существует такой прямоугольник $R$, который содержит все точки из $S$ внутри себя. Поскольку стороны ${R}$ параллельны осям координат, ${R}$ ограничен прямыми $x=\pm a$, $y=\pm b$, где $a,\ b > 0$.
Рассмотрим окружность $\mathcal{C}$, касающуюся справа стороны прямоугольника, лежащей на $x=a$, а также касающуюся $\ell_k$ и $\ell_{k+1}$. Докажем, что эта окружность пересекает $\mathcal{B}$ ровно в $2n - 1$ точках и $\mathcal{R}$ — ровно в ${2n - 1}$ точках.
Поскольку $\mathcal{C}$ касается $\ell_k$ и $\ell_{k+1}$, причем эти прямые разного цвета, достаточно показать, что $\mathcal{C}$ пересекается с любой другой из ${2n - 2}$ прямых ровно в двух точках. Заметим, что никакие две прямые не пересекаются на окружности, поскольку их точки пересечения лежат в $S$, которое находится внутри ${R}$.
Возьмем любую прямую $L$ из этих ${2n - 2}$ прямых. Пусть $L$ пересекает $\ell_k$ и $\ell_{k+1}$ в точках $M$ и $N$, соответственно ($M$ и $N$ могут и совпадать). Заметим, что $M$ и $N$ лежат внутри $R$. Возможны два случая:
$\quad$(i) $L$ пересекает $R$ на $x = -a$ и на $x = a$;
$\quad$(ii) $L$ пересекает $R$ на $y = -b$ и на $y = b$.
Если выполнено (ii), $\angle(\ell_k,L)$ и $\angle(L,\ell_{k+1})$ оба должны быть положительными, и поэтому $\angle(X, L)$ должен находиться между $\angle(X, \ell_k)$ и $\angle(X, \ell_{k+1})$, что приводит к противоречию. Следовательно, выполнено (i). Тогда $L$ пересекает $\mathcal{C}$ ровно в двух точках.
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.