Олимпиада Туймаада по математике. Младшая лига. 2013 год

Для любых положительных чисел $a$ и $b$ докажите неравенство $\sqrt {ab} \le \dfrac{1}{3} \cdot \sqrt {\dfrac{{{a^2} + {b^2}}}{2}} + \dfrac{2}{3} \cdot \dfrac{2}{{\dfrac{1}{a} + \dfrac{1}{b}}}.$ ( А. Храбров )

Комментарий/решение

$$\sqrt{ab}\leq \frac{1}{3}\cdot \sqrt{\frac{a^2+b^2}{2}}+\frac{2}{3}\cdot \frac{2}{\frac{1}{a}+\frac{1}{b}}$$

$$1\leq \frac{1}{3}\cdot \sqrt{\frac{1}{2}\cdot \left(\frac{a}{b}+\frac{b}{a}\right)}+\frac{2}{3}\cdot \frac{2}{\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}}}$$

$$ \sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}}=z\geq 2\Rightarrow \frac{a}{b}+\frac{b}{a}=z^2-2$$

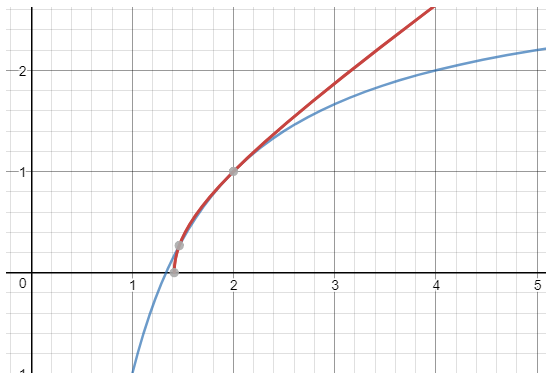
$$\frac{3z-4}{z}\leq \sqrt{\frac{z^2-2}{2}}, \quad z\in[2,+\infty)$$

Соңғы жағын графиксіз былай дәлелдеуге болады:

$\sqrt{\frac{z^2-2}{2}}\ge \frac{3z-4}{z} \iff \frac{z^2-2}{2}\ge \frac{(3z-4)^2}{z^2}$

$\iff z^2(z^2-2)\ge 2(3z-4)^2$

$\iff (z - 2)^2 (z^2 + 4 z - 8)\ge 0$