Районная олимпиада, 2015-2016 учебный год, 11 класс

В треугольнике $ABC$ справедливы следующие соотношения: $AB=5$, $BC=10$ и $\angle ABC=90{}^\circ $. $DEFG$ — квадрат, у которого вершины $D$ и $E$ лежат на отрезке $BC$, вершина $F$ лежит на отрезке $AC$, а вершина $G$ лежит на окружности с центром в точке $A$, проходящей через точку $B$. Найдите площадь $DEFG$.

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Ответ. 4.
Решение. Пусть прямая $FG$ пересекает сторону $AB$ в точке $H$. Сторона $AB=5$ в два раза меньше стороны $BC=10$. Треугольник $CEF$ подобен треугольнику $BCA$. Поэтому если $BH=EF=a$, то $EC=2a$, $DE=a$, $BD=HG=10-3a$, $AH=5-a$ и $AG=AB=5$. Применив теорему Пифагора для треугольника $AGH$, поучим уравнение ${(5-a)^2}+{(10-3a)^2}=25$. Решая квадратное уравнение, получим корни $a_1=2$, $a_2=5$. Второй корень не удовлетворяет условию задачи, так как $5=AB > EF=a$. Следовательно, сторона квадрата $DEFG$ равна 2, а его площадь — 4.

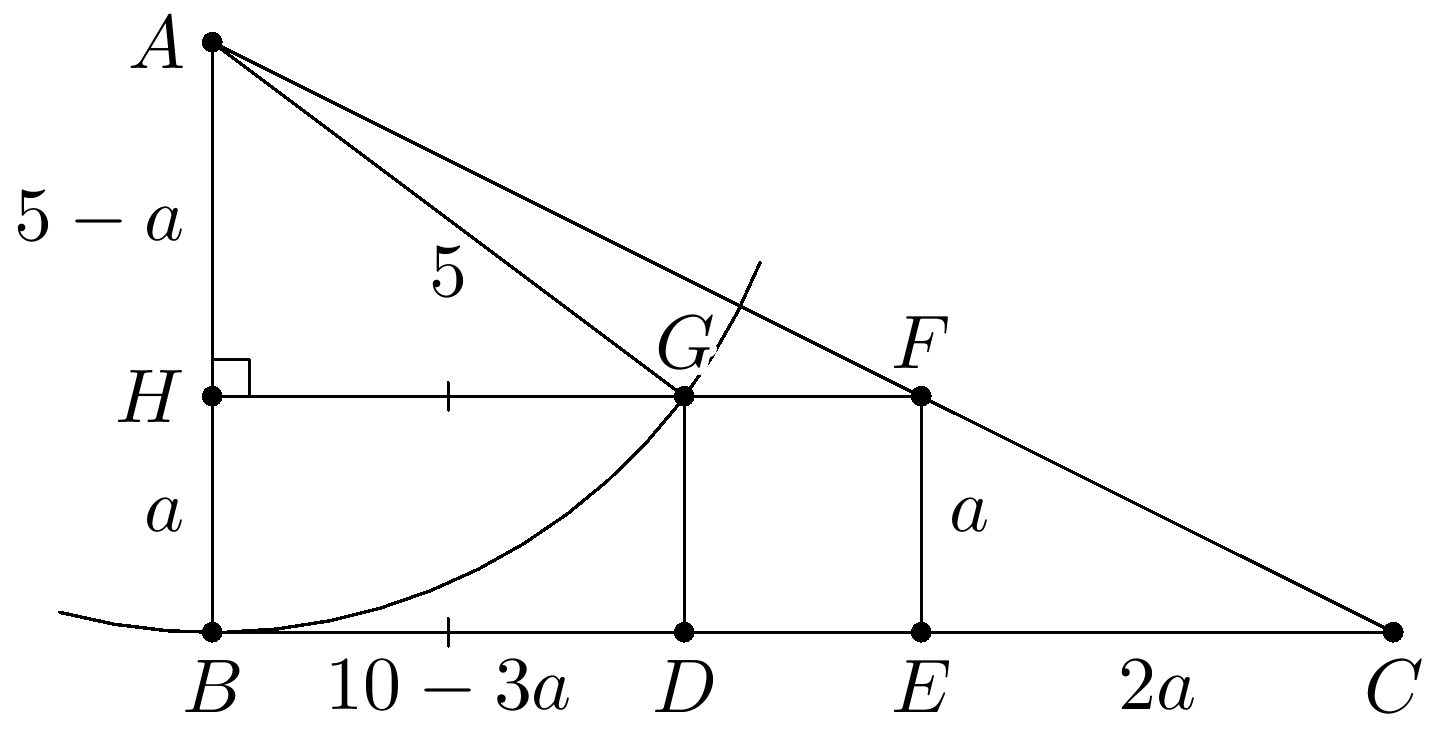
Шешуі:

1) $QK \parallel BD$, $QK = BD$, $AB = QA$, $QK = BD$.

2) Белгілеулер еңгізейік $DE = x$ десек, онда $CE = 2x$, ал $BD = 10 - 3x$ және $AK = 5 - x$ болады. $5 - x > 0 \implies x < 5$.

3) $\triangle QAK$-тан $AQ^2 = KQ^2 + AK^2$ енгіземіз,

$$(5 - x)^2 + (10 - 3x)^2 = 25 \implies x^2 - 7x + 10 = 0.$$

Осынан, $x = 5$ және $x = 2$. $x < 5$ болғандықтан, $DE = 2$ болады. Сонымен, $S_{DEQF} = 22 = 4$.

Жауап: 4