Математикадан республикалық олимпиада, 2015-2016 оқу жылы, 9 сынып
Тор $n \times n$ тақтасын (бұл жерде $n \geq 2$) үш бірлік шаршыдан құралған бұрыштармен келесі шарттар орындалатындай жабамыз (бұрышты шексіз рет $90{}^\circ $-қа бұрса болады):
1) тақтаның кез келген шаршысы кемінде бір бұрышпен жабылған.
2) бір бұрышпен жабылып тұрған ортақ қабырғасы бар екі шаршы, бір уақытта одан басқа шаршымен жабылмаған.
Тақтаны ең көп дегенде қанша шаршымен жабуға болады? ( Ильясов С. )
посмотреть в олимпиаде
1) тақтаның кез келген шаршысы кемінде бір бұрышпен жабылған.
2) бір бұрышпен жабылып тұрған ортақ қабырғасы бар екі шаршы, бір уақытта одан басқа шаршымен жабылмаған.
Тақтаны ең көп дегенде қанша шаршымен жабуға болады? ( Ильясов С. )
Комментарий/решение:
Комментарии от администратора Комментарии от администратора №1.
Ответ. $n(n-1)$.
Будем рассматривать каждый уголок в виде наложения двух доминошек: горизонтального и вертикального (см. рис. ниже).
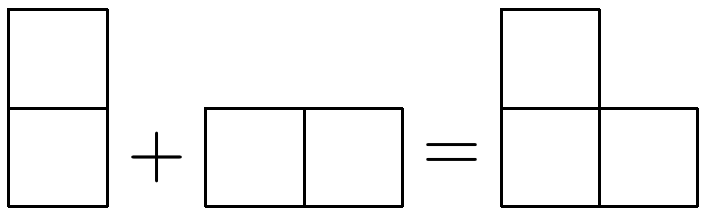
Тогда можно считать, что таблица покрыта доминошкоми по следующим двум правилам:
1) каждая клетка таблицы покрыта хотя бы одной доминошкой.
2) никакая доминошка полностью не покрывает никакую другую.
При таком условии каждая строка или столбец длины $n$ покрываются не более чем $n-1$ доминошкой $2 \times 1$ или $1 \times 2$ соответственно. Поэтому всего доминошек не более чем $2n(n-1)$. Но каждому уголку соответствует $2$ доминошки, поэтому число уголков не более чем $n(n-1)$.
Пример. Строить пример будем по индукции с шагом два.
1) Когда $n=2$ и $n=3$ привести не трудно.
2) Пусть для каждого $k \leq n$ мы показали.
3) Покажем для $k=n+2$.
Рассмотрим ободок ширины 2, полученный из таблицы ${(n+2)}\times{(n+2)}$ путем вырезания центрального квадрата ${(n-2)}\times{(n-2)}$. Поставим уголок (такой как на рис. выше) в нижний левый угол, назовем его первым. Затем переместим его на одну клетку вверх, в новом месте поставим такой же уголок и т.д. В итоге левая часть ободка покрыта ${n+1}$ уголками. Затем переместим первый уголок на одну клетку вправо,в новом месте поставим такой же уголок и т.д. В итоге левая и нижняя часть ободка покрыты ${2n+1}$ уголками. Повернем ободок на $180^\circ $ и проделаем ту же операцию. Таким образом ободок покрыт ${4n+2}$ уголками.
Заметим, что каждый такой уголок покрывает не более одной клетки из центрального квадрата $n \times n$, это означает, что никакой уголок полностью лежащий в центральном квадрате $n \times n$, не противоречит условиям покрытия. Значит в силу предположения индукции центральный квадрат покрывается $n^2-n$ уголками, т.е. таблицу ${(n+2}) \times{( n+2})$ покрыта $n^2-n+4n+2 = n^2 + 3n +2 ={(n+2)}\cdot{(n+1)}$ уголками.

Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.