Олимпиада Туймаада по математике. Старшая лига. 2017 год

На плоскости даны две точки $A$ и $B$. Назовём точку $X$ их нелепой серединой, если на плоскости существует такая декартова система координат, что точки $A$ и $B$ имеют в ней неотрицательные координаты, причем абсцисса точки $X$ в этой системе равна среднему геометрическому абсцисс точек $A$ и $B$, а ордината — среднему геометрическому ординат $A$ и $B$. Найдите геометрическое место всех нелепых середин точек $A$ и $B$. ( К. Тыщук )

Комментарий/решение

Ответ: ГМТ "нелепых середин" - часть плоскости , ограниченная окружностью (внутри), построенной на $AB$ как на диаметре

1) Пусть координаты точек $A$ и $B$ в произвольной ПДСК (прямоугольной декартовой системе координат) будут:

$$A(x_A;y_A);\;\;\;\;B(x_B;y_B);$$

2) Среднее геометрическое чисел $a$ и $b$ : $GM = \sqrt{a\cdot b}$

Среднее арифметическое чисел $a$ и $b$ : $AM = \dfrac{a+b}{2}$

По неравенству о средних $AM \ge GM$

3) В этой же ПДСК по условию задачи координаты точки $X$

$$X(\sqrt{x_A\cdot x_B};\sqrt{y_A\cdot y_B})$$

4) Согласно (2) Можно получить выражения для ГМТ точек $X$ при фиксированной угловой ориентации вектора $\overrightarrow{AB}$ и выбранной ПДСК

$$\min(x_A;x_B)=\sqrt{\min(x_A;x_B)\cdot \min(x_A;x_B)}<\sqrt{x_A \cdot x_B}<\dfrac{x_A + x_B}{2}$$

$$\min(y_A;y_B)=\sqrt{\min(y_A;y_B)\cdot \min(y_A;y_B)}<\sqrt{y_A \cdot y_B}<\dfrac{y_A + y_B}{2}$$

Геометрически, точки $X$ лягут в область $G$ (см. рис.)

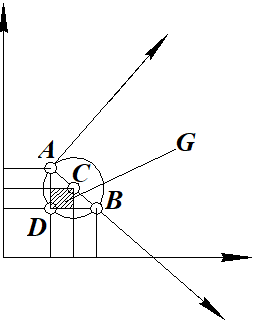
Пусть $C - $ середина отрезка $AB$. Построим прямоугольный треугольник $ADB$. Точка $D$ будет лежать на окружности, построенной на $AB$ как на диаметре . Остается показать, что отрезок $CD$ может иметь угол от 0 до 360 градусов по отношению к $\overrightarrow{AB}$. Это так, потому что произвольно выбирали наклон ПДСК к $\overrightarrow{AB}$ . Отрезок $CD$ заметает все точки внутри окружности