16-я Международная Жаутыковская олимпиада по математике, 2020 год

В неравнобедренном треугольнике $ABC$ точка $I$ — центр вписанной окружности, а $CN$ — биссектриса. Прямая $CN$ вторично пересекает описанную окружность треугольника $ABC$ в точке $M$. Прямая $\ell$ параллельна прямой $AB$ и касается вписанной окружности треугольника $ABC$. Точка $R$ на прямой $\ell$ такова, что $CI \perp IR$. Описанная окружность треугольника $MNR$ вторично пересекает прямую $IR$ в точке $S$. Докажите, что $AS=BS$. ( М. Кунгожин )

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Напомним, что ориентированным углом между прямыми $n$ и $m$ называется такой угол, на который нужно против часовой стрелки повернуть прямую $n,$ чтобы она стала параллельна прямой $m.$ Обозначается ориентированный угол через $\angle (n, m).$ Проведем из точки $N$ касательную прямую $d$, отличную от $AB$, ко вписанной окружности $\triangle ABC$. Тогда $\angle (\ell,CI)=\angle (NB,NI)=\angle (NI,d)$. Так как $CI \perp IR$, то в силу симметрии относительно прямой $IR$ прямая $d$ проходит через точку $R$. Пусть прямые $MS$ и $\ell$ пересекаются в точке $T$. Тогда $\angle (MN,MS)=\angle (RN,RS)=\angle (RS,RT)$, то есть точки $R,$ $T$, $I$, $M$ лежат на одной окружности. Поэтому из $\angle (RI,MI)=90^\circ$, следует $\angle (RT,MT)=90^\circ$. Значит, $MS \perp AB$. Но, так как $M$ лежит на серединном перпендикуляре отрезка $AB$, то и $S$ также лежит на нем. Следовательно, $AS=BS $.

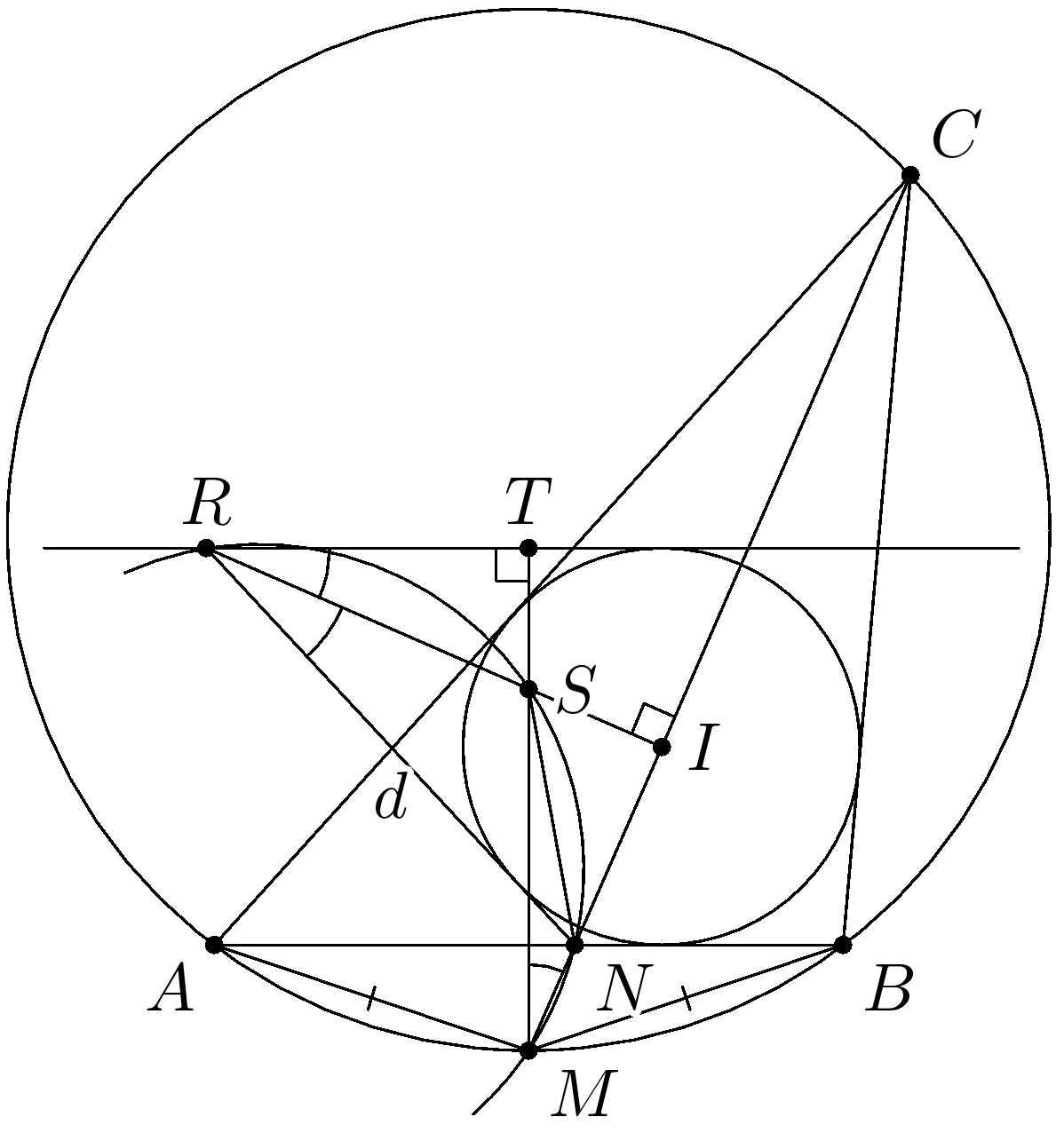
пусть $D$ и $E$ точки пересечения прямой $l$ с $AC$ и $BC$ соответственно. Так как $l$ касается вписанной окружности то $DI$ и $EI$ биссектрисы углов $ADE$ и $BED$. Пусть $\angle CAB = 2a$, then $\angle EDA = 180-2a$ откуда следует что $DI \bot AI$ аналогично $EI \bot BI$. Пусть $A'$ and $B'$ пересечение $l$ с прямыми $AI$ and $BI$, тогда так как $AI=IA'$ and $BI=IB'$ выходит что $AB'A'B$ параллелограмм. Пусть $K$ и $T$ точки пересечения $l$ с $CM$ и $MS$. По подобию легко заметить что $KI=NI$, то есть $\angle KRI = \angle NRI = \angle IMT$, и так как $RI \bot MI$ то $RT \bot MS$, и $l \parallel AB$ значит $MS \bot AB$, $S$ лежит на серединном перпендикуляре $AB$, т.к $M$ также лежит на серединном перпендикуляре $AB$, это значит что $AS=BS$