17-я Международная Жаутыковская олимпиада по математике, 2021 год

Дан выпуклый вписанный шестиугольник $ABCDEF$, в котором $BC=EF$ и $CD=AF$. Диагонали $AC$ и $BF$ пересекаются в точке $Q$, а диагонали $EC$ и $DF$ — в точке $P$. На отрезках $DF$ и $BF$ отмечены точки $R$ и $S$ соответственно так, что $FR=PD$ и $BQ=FS$. Отрезки $RQ$ и $PS$ пересекаются в точке $T$. Докажите, что прямая $TC$ делит диагональ $DB$ пополам. ( М. Кунгожин )

Комментарий/решение

Решение: Сперва приведем очевидные свойства (попробуйте доказать самостоятельно, это довольно просто):

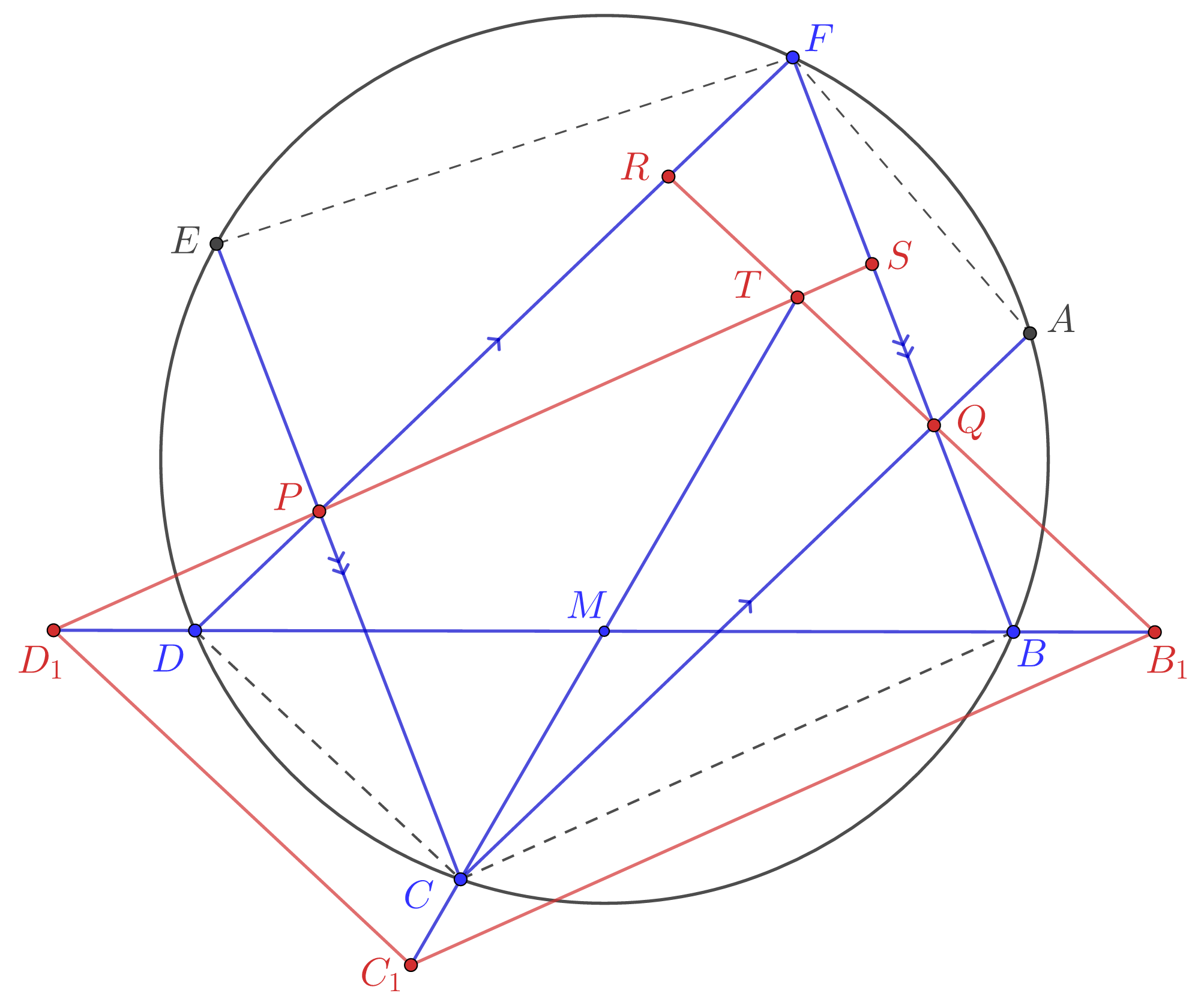
Свойство 1: $FPCQ$ $-$ параллелограмм.

Свойство 2: $RDCQ$ и $SBCP$ $-$ параллелограммы.

Далее введем точки $D_1=(SP \cap DB)$ и $B_1=(RQ \cap BD).$ Из теоремы Менелая для:

$(i)\quad \triangle DFB$ и $(S,P,D_1):$ $\dfrac{BD_1}{DD_1}\cdot\dfrac{DP}{FP}\cdot\dfrac{FS}{BS}=1,$

$(ii)\quad \triangle DFB$ и $(R,Q,B_1):$ $\dfrac{DB_1}{BB_1}\cdot\dfrac{BQ}{FQ}\cdot\dfrac{FR}{DR}=1.$

Из этих двух равенств легко следует, что $DD_1=BB_1.$ $($Так как $DP=FR,BQ=FS,FP=DR,BS=FQ.)$

Пусть $M$ $-$ середина отрезка $BD.$ Рассмотрим гомотетию с центром в $M$ такую, что $D\to D_1,$ тогда очевидно, что $B\to B_1.$ Если $C\to C_1,$ то

$$D_1C_1\parallel DC\parallel TB_1 \quad \text{и} \quad B_1C_1\parallel BC\parallel TD_1\implies TB_1C_1D_1-\text{параллелограмм.}$$

Следовательно точки $T,M,C,C_1$ лежат на одной прямой, иными словами прямая $TC$ делит диагональ $DB$ пополам.$\quad\blacksquare$

В какой программе вы делаете чертежи?

GeoGebra Geometry

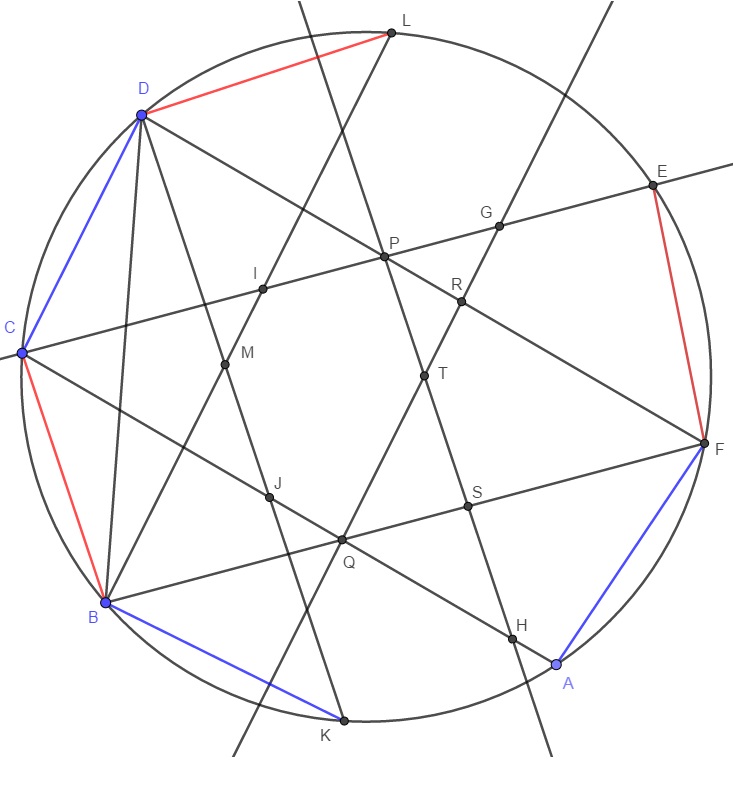
$ACDF, BCEF$ равнобедренные трапеции из условия, так как $AC || DF, BF || CE$ тогда $PS || BC , RQ || CD$ и $PS=BC, RQ=CD$ по равенству треугольников $PCF, BCQ$ и $CDP, FRQ$ по построению. Окружность $\omega$ пусть $BL ||CD , \ L \in \omega$ и $DK || BC, \ K \in \omega$ если $I \in \ CE \cap BL, \ G \in QR \cap CE, H \in \ PS \cap AC , \ J \in DK \ \cap AC$ и $M \in DK \cap BL$

Лемма: треугольники $CGH, CIJ$ подобны.

Доказательство: докажем что $\dfrac{CI}{CG} = \dfrac{CJ}{CH}$ из соответственных треугольников

$CG = \dfrac{CQ \cdot \sin CDP}{\sin PCD}$ и $CI = \dfrac{BC \cdot \sin CBL}{\sin PCD}$

и так как $\dfrac{CQ}{BC} = \dfrac{\sin CDP}{\sin CQB}$ (все углы использовались из параллельности нужных прямых следующих из построения)

тогда $\dfrac{CI}{CG} = (\dfrac{\sin CPD}{\sin CDP})^2 = (\dfrac{CD}{CP})^2$

Аналогично

$CH = \dfrac{CP \cdot \sin CBQ}{\sin BCQ}$

$CJ = \dfrac{CD \cdot \sin CDK}{\sin BCQ}$

то есть $\dfrac{CJ}{CH}= (\dfrac{\sin CPD}{\sin CDP})^2 = (\dfrac{CD}{CP})^2$

Тогда $C,M,T$ лежат на одной прямой, значит $CM$ делит $BD$ пополам, так как $BCDM$ параллелограмм.

Поменяем местами $R$ и $S$. $SQ \cap BD=K, RP \cap BD=M$

Из двух теорем менелая можно легко понять что $BK=DM$. Из Ratio lemma остается доказать что $\frac{\sin KTC}{\sin MTC}=\frac{TM}{TK}$.

Из теорем синусов в треугольниках $CQT, CPT$ выходит что $\frac{\sin KTC}{\sin MTC}=\frac{QC*\sin CQT}{CP*\sin CPT}$. Очевидно что $CQRP, CQDS,FCPQ$ параллелограммы. Отсюда $\sin CPT=\sin EPT=\sin EFR=\sin AFS=\sin CQT$ значит $\frac{\sin KTC}{\sin MTC}=\frac{QC}{CP}$.

$\frac{TM}{TK}=\frac{\sin BKQ}{\sin DMP}$. Из двух теорем синусов в треугольниках $BKQ,DMP$. Выходит что

$\frac{\sin BKQ}{\sin DMP}=\frac{\sin BKQ*BQ}{\sin DPM*DP}$. Из двух теорем синусов в треугольниках $FSQ,FPR$ выходит что $\frac{\sin BQK}{\sin DPM}=\frac{FS*RP}{QS*RF}$=>> (!) $\frac{QC}{CP}=\frac{RP}{QS}$. Что верно так как дуги $AE$ и $BD$ равны.