Олимпиада имени Леонарда Эйлера 2021-2022 учебный год, I тур заключительного этапа
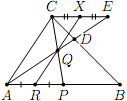
На стороне $BC$ треугольника $ABC$ отмечена точка $D$. На стороне $AB$ выбрана точка $P$. Отрезки $PC$ и $AD$ пересекаются в точке $Q$. Точка $R$ — середина отрезка $AP$. Докажите, что существует фиксированная точка $X$, через которую прямая $RQ$ проходит при любом выборе точки $P$.
(
А. Кузнецов
)
посмотреть в олимпиаде
Комментарий/решение:
Комментарии от администратора Комментарии от администратора №1.
Решение. Проведем через точку $C$ прямую, параллельную прямой $AB$, и пусть $E$ — точка ее пересечения с прямой $AD$. Искомая точка $X$ — это середина отрезка $CE$. В самом деле, точки $R$, $Q$ и $X$ лежат на одной прямой при любом выборе точки $P$ как середины сторон и точка пересечения диагоналей трапеции $APEC$.
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.