Областная олимпиада по математике, 2004 год, 9 класс

В данном множестве $A$ целых положительных чисел верно условие: для любых различных $x, y \in A$ выполняется неравенство $|x-y|\geq \frac{xy}{30}$. Какое максимальное количество элементов может содержать данное множество $A$?

Комментарий/решение

$$\textbf{1)} x>y\Rightarrow x-y\geq \frac{xy}{30}\Rightarrow x(30-y)\geq 30y\Rightarrow 30\geq y >0$$

$$\textbf{2)} x<y\Rightarrow y-x\geq \frac{xy}{30}\Rightarrow y(30-x)\geq 30x\Rightarrow 30\geq x >0$$

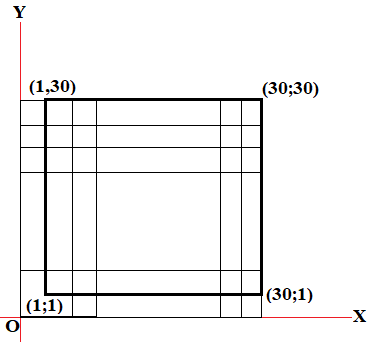
$$\alpha_{xy}=(x,y) \Rightarrow XY=\begin{pmatrix} \alpha_{11} & \alpha_{12} & ...& \alpha_{1,30}\\ \alpha_{21} & \alpha_{22} & ...& \alpha_{2,30} \\ ...&...&...&...\\\alpha_{30,1} & \alpha_{30,2} & ...& \alpha_{30,30}\end{pmatrix}$$

$$x\ne y \Rightarrow XY- diag \left\{XY\right\}=\begin{pmatrix} 0& \alpha_{12} & ...& \alpha_{1,30}\\ \alpha_{21} & 0 & ...& \alpha_{2,30} \\ ...&...&...&...\\\alpha_{30,1} & \alpha_{30,2} & ...& 0\end{pmatrix}$$

$$\sum_{max} \left(XY-diag \left\{XY\right\}\right) = \begin{Vmatrix} 0 & \alpha_{12} & ...& \alpha_{1,30}\\ \alpha_{21} & 0 & ...& \alpha_{2,30} \\ ...&...&...&...\\\alpha_{30,1} & \alpha_{30,2} & ...& 0\end{Vmatrix}=30^2-30=870$$

$$\textbf{OTBET:}870$$

БОО $x>y$, тогда $$30x-30y \geq xy,$$ $30x-xy-30y+900 \geq 900$, $x(30-y)+30(30-y)=(30-y)(30+x) \geq 900$. Если есть хотя бы $870$ таких чисел, то найдутся такие $x$ и $y$, что $x,y>30$, тогда $(30-y)(30+x) \geq 900$ не выполняется, так как $30-y$ будет отрицательным, а $30+x$ - нет, противоречие

БОО $x>y$, тогда $$30x-30y \geq xy,$$ $30x-xy-30y+900 \geq 900$, $x(30-y)+30(30-y)=(30-y)(30+x) \geq 900$. Допустим, что у нас есть хотя бы $31$ чисел, тогда найдутся $x$ и $y$, что $x>y \geq 30$, тогда для этих $x$ и $y$ имеем $900 \leq (30-y)(30+x) \leq 0$, противоречие. Отсюда следует, что чисел максимум $30$. Далее рассмотрим числа $6$ и $7$, они не могут одновременно присутствовать в нашем множестве, так как $24*37=288<900$. Оставим число $6$ для наибольшего количества чисел в нашем множестве, следующее число - $8$. Если следующее число $8$, тогда чисел $9$ и $10$ не может быть, следующее число - $11$ и т.д. Итого получаем числа $1,2,3,4,5,6,8,11,18, 45$.

Ответ:$10$