Республиканская олимпиада по математике, 2023 год, 9 класс
Дана клетчатая доска $2n\times 2n$. Самат закрашивает некоторые клетки в синий или в красный цвет. Он должен раскрасить ровно $k$ клеток. Фархат раскрашивает все остальные клетки доски в синий или красный цвет так, чтобы итоговая доска удовлетворяла следующим условиям:
в каждой строке и в каждом столбце одинаковое количество синих и красных клеток;
в каждой строке и в каждом столбце нет трех последовательных клеток одного цвета;
любые две строки различны и любые два столбца различны. (Если у строк $r_1$ и $r_2$ есть клетки разного цвета, находящиеся в одном столбце, то эти строки считаются различными. Аналогично и для столбцов.)
Найдите наименьшее возможное значение $k$ (в зависимости от $n$), при котором Фархат может покрасить доску не более чем одним способом независимо от раскраски Самата. (Если клетка уже покрашена в синий или в красный цвет, то его больше нельзя перекрашивать.) ( Сам Ф. )
посмотреть в олимпиаде
в каждой строке и в каждом столбце одинаковое количество синих и красных клеток;
в каждой строке и в каждом столбце нет трех последовательных клеток одного цвета;
любые две строки различны и любые два столбца различны. (Если у строк $r_1$ и $r_2$ есть клетки разного цвета, находящиеся в одном столбце, то эти строки считаются различными. Аналогично и для столбцов.)
Найдите наименьшее возможное значение $k$ (в зависимости от $n$), при котором Фархат может покрасить доску не более чем одним способом независимо от раскраски Самата. (Если клетка уже покрашена в синий или в красный цвет, то его больше нельзя перекрашивать.) ( Сам Ф. )
Комментарий/решение:
Ответ: $4n^2-3.$ Из первого условия выходит однозначность.
Теперь пример для $4n^2-4$. Главная идея заключается в том, что если перекрасить шахматный квадратик $2\times 2$ (или любые 4 точки которые образуют шахматный прямоугольник), то это сохранит условие 1 и почти сохраняет условия 2 и 3. Осталось придумать пример. Когда $n=1$ или $n=2:$
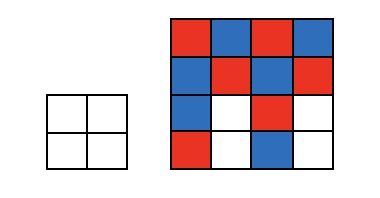
Когда $n>2$ разбиваем на четный и нечетный случай (слева для четных $n$, справа для нечетных):
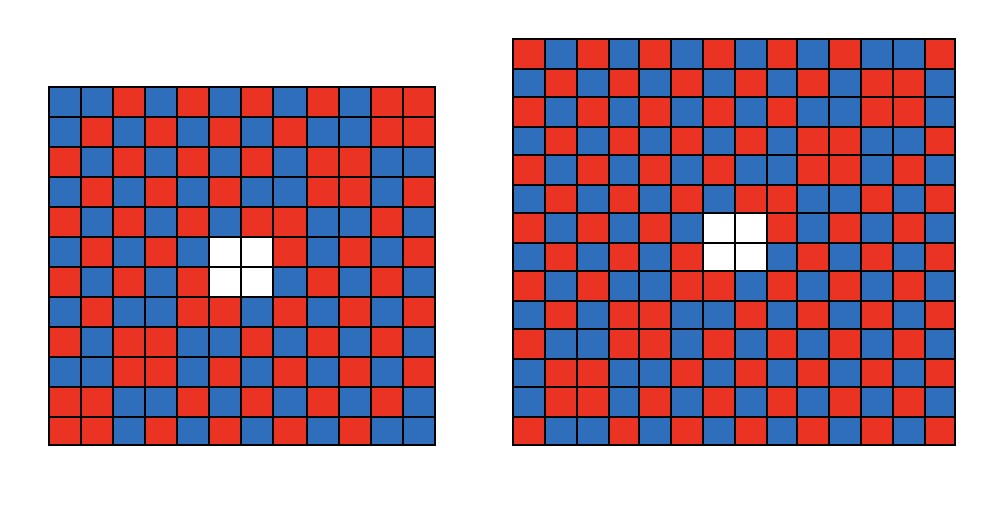
И не закрашенные клетки можно раскрасить двумя шахматными способами.
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.