Республиканская олимпиада по математике, 2023 год, 9 класс

\q3 Өлшемі $2n\times 2n$ ұяшықты тақта берілген. Самат тақтаның кейбір ұяшықтарын көк немесе қызыл түске бояйды. Ол жалпы дәл $k$ ұяшықты бояу керек. Содан кейін Фархат қалған барлық боялмаған ұяшықтарды көк немесе қызыл түске келесі шарттар орындалатындай бояйды:
   әр қатарда және әр бағанда көк және қызыл ұяшықтар саны тең;
   ешқандай қатарда және ешқандай бағанда қатар келген бір түсті үш ұяшық жоқ;
   кез келген екі қатар әртүрлі және кез келген екі баған әртүрлі. (Егер $r_1$ және $r_2$ қатарларының бір бағанда жататын әртүрлі түсті екі ұяшығы табылса, ондай $r_1$ және $r_2$ қатарларын әртүрлі деп есептейміз. Дәл сол сияқты баған үшін әртүрлі бағандарды анықтаймыз.)
   Фархат Саматтың қалай бояғанына қарамастан тақтаны ең көп дегенде бір әдіспен ғана бояй алатындай $n$-ге тәуелді ең кіші мүмкін $k$ санын табыңыз. (Ұяшықты бірінші рет бояғаннан кейін үстінен тағы бояуға болмайды.) ( Сам Ф. )

Комментарий/решение

Ответ: $4n^2-3.$ Из первого условия выходит однозначность.

Теперь пример для $4n^2-4$. Главная идея заключается в том, что если перекрасить шахматный квадратик $2\times 2$ (или любые 4 точки которые образуют шахматный прямоугольник), то это сохранит условие 1 и почти сохраняет условия 2 и 3. Осталось придумать пример. Когда $n=1$ или $n=2:$

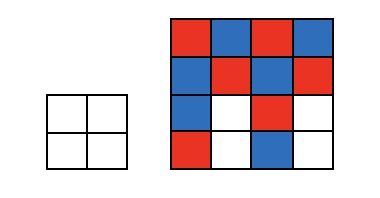
Когда $n>2$ разбиваем на четный и нечетный случай (слева для четных $n$, справа для нечетных):

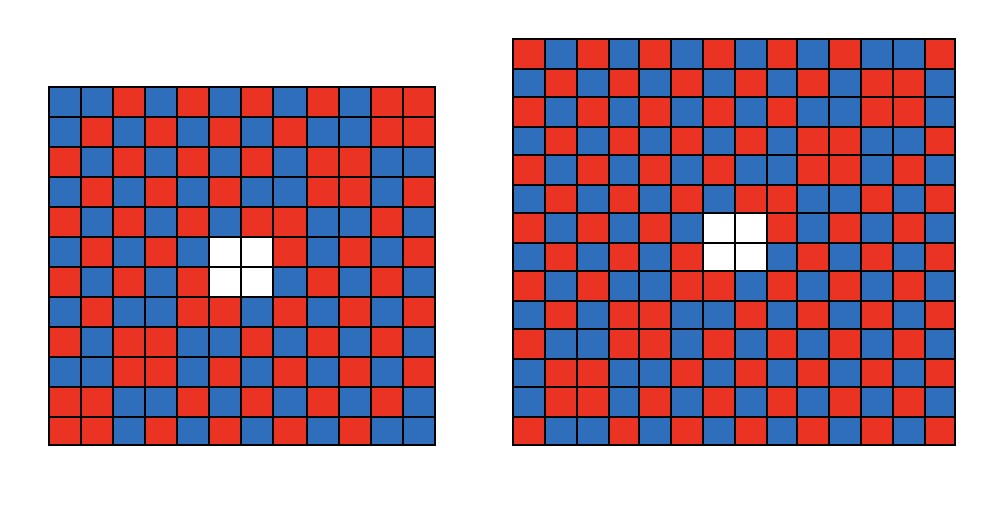
И не закрашенные клетки можно раскрасить двумя шахматными способами.