10-я международная Иранская олимпиада по геометрии, 2023 год, вторая лига, 9-10 классы

Точки $M$ и $N$ — середины сторон $AB$ и $BC$ квадрата $ABCD$ (см. рисунок ниже). Согласно рисунку, нарисованы правильный шестиугольник и правильный 12-угольник. Точки $P$, $Q$ и $R$ — центры этих трех многоугольников. Докажите, что $PQRS$ — вписанный четырёхугольник.

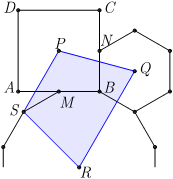
Комментарий/решение

Подсказка:

Любой правильный $n$-угольник можно вписать в окружность, и если вписать многоугольники с центрами $R$ и $Q$ получим, что общая сторона $12$-угольника и $6$-угольника-радикальный ось этих окружностей

$S'\text{ } -\text{ }$ точка симметричная $\text{ }S\text{ }$ относительно перпендикуляру к $\text{ }MB\text{ }$ из $\text{ }R$

Мое решение на олимпе: ( правда оно не получило полные баллы )

Очевидно $:BS' \perp QR$

\[ \]

Утверждение: $PS \parallel QR$

Доказательство: $\angle PSS' = \angle MSP + \angle MSS' = \dfrac{180 - \angle SMP}{2} + 30^\circ = 60^\circ; \text{ } \text{ } \text{ } \angle SS'B = 30^\circ \text{ } \text{ } \text{ } \blacksquare $

\[ \]

Осталось доказать что$:$ $SR = PQ$

Заметим$:$ $\text{ } \triangle RMS' \text{ } - \text{ }$ равносторонний; $\text{ } QS' \text{ }$ параллелен и равен $\text{ } PM\text{ }\rightarrow PQ = MS' \text{ } \text{ }\text{ }\square$

Думаю, нужно было более открыто расписать последнюю и предпоследнюю строчку. У меня тоже самое, но я чтобы доказать последнее, я построил дофига прямоугольных треугольников и добил тригонометрией, получил фулл за 1

Осталось доказать что $: SR=PQ$ т.к. тогда это будет равнобокая трапеция

$\angle RMS' = \dfrac{360}{12}^\circ \times 2 = 60^\circ$ также $RM = RS' \rightarrow \triangle RMS' -$ равностороний

$QS' \parallel PM; QS'=PM \rightarrow QS'MP -$ параллелограм

Значит$:$ $ MS'=PQ $

$MS'=MR=SR \text{ } \text{ } \text{ }\square$

Кстати надо еще доказать что $SR \nparallel PQ$ но это уже слишком очевидно

Переформулируем условие (для простоты без лишних обозначений):

Дан квадрат 1 (расположим, чтобы стороны смотрели равно по сторонам света), снизу достроим квадрат 2, с остальных сторон (влево, вверх, вправо) во вне построим правильные треугольники 3, 4, 5 соответственно. Слева и справа вне 2 построим правильные треугольники 6 и 7. Требуется показать, что следующие вершины лежат на одной окружности: верх 4, право 5, низ-право 2 и лево 6.

По второй теореме Тебо для 1, 4 и 5 получим, что от верха 4 до права 5 столько же сколько от низ-лево 1 до верх 4, а это столько же (из того, что объединение 1 и 4 равно объединению 2 и 6), сколько от низ-право 2 до лево 6.

Заметим, что выпуклая оболочка объединения 1, 2, 3, 5, 6, 7 имеет центр симметрии, а еще что выпуклая оболочка 3 и 6 (5 и 7 аналогично) - половинка правильного шестиугольника, тем самым прямая $\aleph$ от лево 6 до верх-лево 1 делит верхний угол 3 пополам, значит $30^\circ+60^\circ+90^\circ=180^\circ$, то есть прямая $\aleph$ проходит и через верх 4, более того $\aleph$ параллельна прямой от низ-право 2 до право 5.

Исходя из этого, нужная фигура - равнобокая трапеция, поэтому около нее можно описать окружность.