10-я международная Иранская олимпиада по геометрии, 2023 год, вторая лига, 9-10 классы
Задача №1. Точки $M$ и $N$ — середины сторон $AB$ и $BC$ квадрата $ABCD$ (см. рисунок ниже). Согласно рисунку, нарисованы правильный шестиугольник и правильный 12-угольник. Точки $P$, $Q$ и $R$ — центры этих трех многоугольников. Докажите, что $PQRS$ — вписанный четырёхугольник.
комментарий/решение(5)
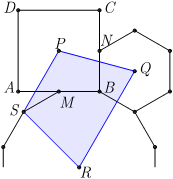
комментарий/решение(5)
Задача №2. Дан выпуклый шестиугольник $ABCDEF$ с точкой $P$ внутри него. Предположим, что $BCEF$ — это квадрат, и $ABP$ и $PCD$ — прямоугольные равнобедренные треугольники с прямыми углами в вершинах $B$ и $C$. Прямые $AF$ и $DE$ пересекаются в точке $G$. Докажите, что $GP \perp BC$.
комментарий/решение(1)
комментарий/решение(1)
Задача №3. Пусть $\omega$ — описанная окружность треугольника $ABC$ с соотношением углов $\angle B=3\angle C$. Внутренняя биссектрисса угла $\angle A$ пересекает $\omega$ и $BC$ в точках $M$ и $D$ соответственно. Точка $E$ лежит на продолжении прямой $CM$ за точкой $M$ (то есть $M$ лежит между $C$ и $E$) так, что $ME$ равен радиусу $\omega$. Докажите, что окружности, описанные около треугольников $ACE$ и $BDM$, касаются.
комментарий/решение(2)
комментарий/решение(2)
Задача №4. Пусть $P$ — середина дуги $BAC$ описанной окружности треугольника $ABC$. Высоты треугольника $ABC$ пересекаются в точке $H$. Точки $Q$ и $S$ таковы, что $HAPQ$ и $SACQ$ — параллелограммы. Пусть $T$ — середина $AQ$, а $R$ — точка пересечения прямых $SQ$ и $PB$. Докажите, что прямые $AB$, $SH$ и $TR$ пересекаются в одной точке.
комментарий/решение
комментарий/решение
Задача №5. Даны $n$ точек на плоскости так, что по крайней мере $99\%$ четырёхугольников с вершинами из этих точек являются выпуклыми. Можно ли найти выпуклый многоугольник в плоскости, у которого по крайней мере $90\%$ вершин совпадают с данными точками?
комментарий/решение
комментарий/решение