Математикадан республикалық олимпиада, 1998-1999 оқу жылы, 10 сынып

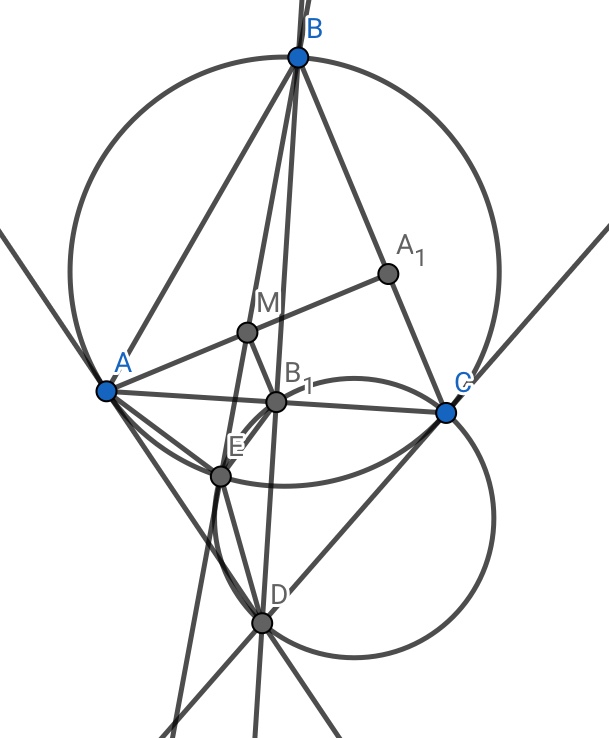
Табаны $AC$ болатын сүйір бұрышты тең бүйірлі $ABC$ үшбұрышында $A{{A}_{1}}$ және $B{{B}_{1}}$ биіктіктері жүргізілген. $B$ төбесі және $A{{A}_{1}}$ кесіндінің ортасы арқылы өтетін түзу $ABC$ үшбұрышына сырттай сызылған $T$ шеңберді $E$ нүктесінде қияды. $T$-ға $A$ нүктесінен жүргізілген жанама $B{{B}_{1}}$ тузуін $D$ нүктесінде қияды. $D$, $E$, ${{B}_{1}}$ және $C$ нүктелері бір шеңбердің бойында жататынын дәлелде.

Комментарий/решение

$MB_{1}$ средняя линия $\Delta AA_{1}C$ значит $\angle EMB_{1} = \angle EBC = \angle EAC$ откуда $AMB_{1}E$ вписанный, из условия следует что $CD$ так же касательная, требуется доказать что $\angle DCE = \angle DB_{1}E$ что верно, так как $\angle DCE= \angle CBE$ и $\angle DB_{1}E = 90^{\circ} - \angle AB_{1}E = 90^{\circ} - \angle AME = \angle CBE$.