Математикадан республикалық олимпиада, 2003-2004 оқу жылы, 9 сынып

Сүйірбүрышты $ABC$ үшбұрышында $D$ нүктесі — $C$ төбесінен түсірілген биіктіктің табаны, ал $M$ — $AB$ қабырғасының ортасы. $M$ нүктесі арқылы өтетін түзу $CA$ және $CB$ сәулелерін сәйкес $K$ және $L$ нүктелерінде $CK=CL$ болатындай етіп қияды. Енді $S$ арқылы $SKL$ үшбұрышына сырттай сызылған шеңбердің центрірін белгілейік. Онда $SD=SM$ екенін дәлелдеңіз.

Комментарий/решение

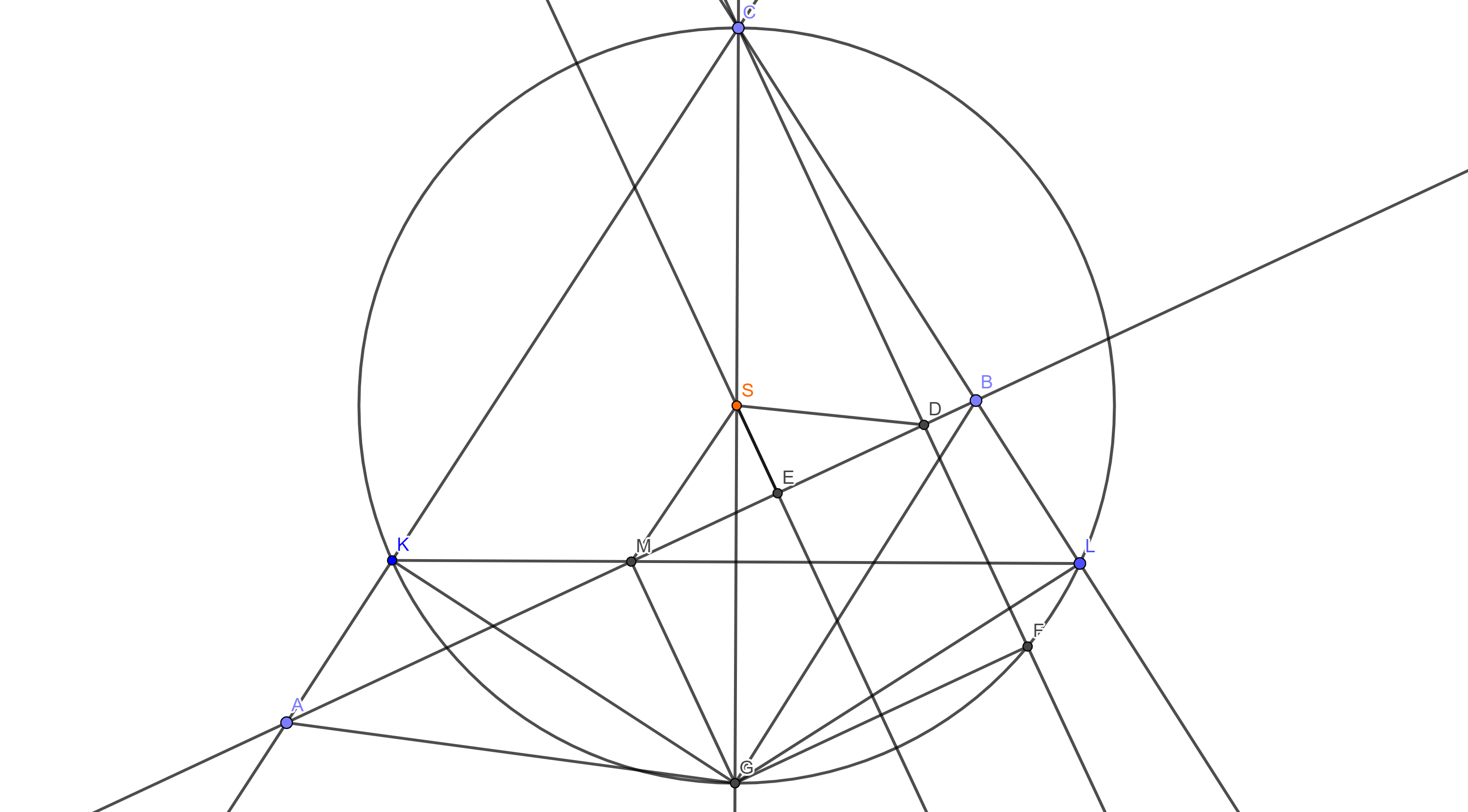
Проведем прямую $SE$, параллельную $CD$, по теореме синусов для $\triangle AKM$ получаем, что $\frac{AM}{sin \alpha}=\frac{AK}{sin \beta}$, а для $\triangle MBL$ - $\frac{MB}{sin (180-\alpha)}=\frac{BL}{sin \beta}$, отсюда следует, что $AK=BL$

Рассмотрим треугольники $AKG$ и $GBL$, они равны, так как $AK=BL, GK=GL, \angle AKG=\angle GLB=90, \Rightarrow GA=GB,$ но $AM=MG$, $\Rightarrow MG \bot AB$, тогда $MDFG$ - прямоугольник, $SG=SF$, поэтому $SE$ делит $GF$ пополам, $\Rightarrow SE$ делит и $MD$ пополам, то есть $SM=SD$