Математикадан республикалық олимпиада, 2005-2006 оқу жылы, 10 сынып
Комментарий/решение:
Доказательство
1) Представим $x$ в виде $x=2\pi\cdot k+\varphi$ где $k\in\mathbb N,\varphi\in (0;2\pi)$
2) Заметим, что $\sin x=\sin (2\pi\cdot k+\varphi)=\sin\varphi$
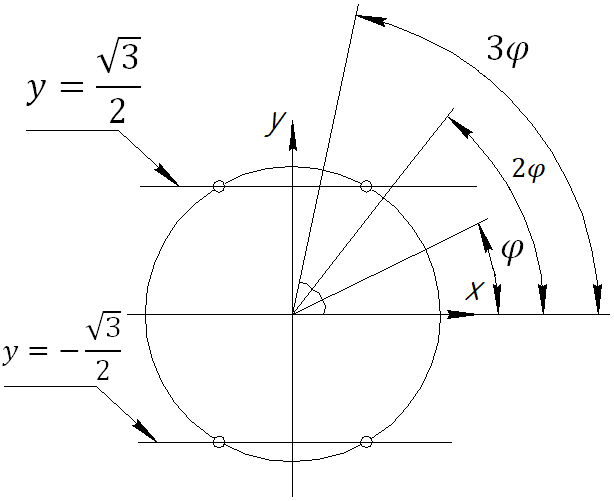
3) Рассмотрим углы $x,2x,3x,...,mx$
$$2x=4\pi\cdot k+2\varphi\rightarrow \sin 2x=\sin2\varphi$$
$$3x=6\pi\cdot k+3\varphi\rightarrow \sin 3x=\sin3\varphi$$
Не буду доказывать по индукции, и так ясно, что
$$mx=2m\pi\cdot k+m\varphi\rightarrow \sin mx=\sin m\varphi$$
4) Если $\varphi\in \left[\dfrac{\pi}{3};\dfrac{2\pi}{3}\right]\cup\left[\dfrac{4\pi}{3};\dfrac{5\pi}{3}\right]$, то $|\sin x| =| \sin\varphi| \ge \dfrac{\sqrt 3}{2}$ и $n=1$
5) Если $\varphi\in \left(0;\dfrac{\pi}{3}\right)$, то можно суммировать к углу $\varphi$ добавлять еще $\varphi$, и так до тех пор, пока не поднимемся выше прямой $\dfrac{\sqrt 3}{2}$ на единичной прямой (см рисунок).
6) Если $\varphi\in \left(-\dfrac{\pi}{3};0\right)$, то можно суммировать к углу $\varphi$ добавлять еще $\varphi$, и так до тех пор, пока не спустимся выше прямой $-\dfrac{\sqrt 3}{2}$ на единичной прямой (см рисунок)
7) При остальных углах тоже можно добиться последовательным прибавлением углов добиться $|\sin x| =| \sin\varphi| \ge \dfrac{\sqrt 3}{2}$
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.