2-я международная Иранская олимпиада по геометрии, 2015 год, вторая лига, 9-10 классы

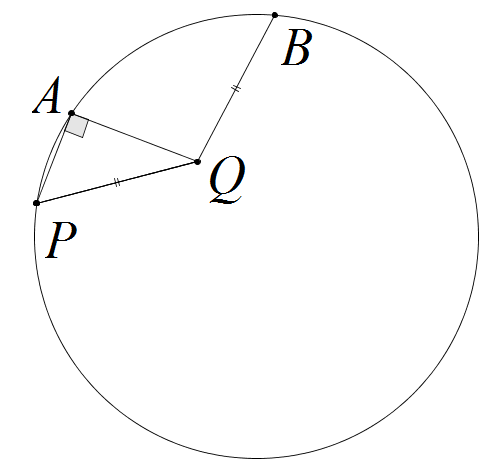
Задача №1.  На рисунке ниже точки $P, A, B$ лежат на окружности, а точка $Q$ внутри окружности так, что $\angle{PAQ}=90^\circ$ и $PQ=BQ$. Докажите, что значение разности углов $\angle{AQB}-\angle{PQA}$ равна центральному углу, опирающемуся на дугу $AB$.

комментарий/решение(4)

---

Задача №2.  В остроугольном треугольнике $ABC$ проведена высота $BH$ из вершины $B$. Точки $D$ и $E$ являются серединами сторон $AB$ и $AC$ соответственно. Пусть точка $F$ симметрична точке $H$ относительно прямой $ED$. Докажите, что прямая $BF$ проходит через центр описанной окружности $\triangle ABC$.
комментарий/решение(2)

---

Задача №3.  В треугольнике $ABC$ точки $M, N, K$ являются серединами сторон $BC, CA, AB$ соответственно. На сторонах $AC$ и $AB$ как на диаметрах во внешнюю сторону построены две полуокружности $\omega_B$ и $\omega_C$ соответственно. Предположим, что прямые $MK$ и $MN$ пересекают $\omega_C$ и $\omega_B$ в точках $X$ и $Y$ соответственно. Пусть касательные прямые в точках $X$ и $Y$ к $\omega_C$ и $\omega_B$ соответственно пересекаются в точке $Z$. Докажите, что $AZ \bot BC$.
комментарий/решение(1)

---

Задача №4.  В окружность $\omega$ с центром $O$ вписан правильный треугольник $ABC$. Пусть $P$ — точка дуги $BC$. Касательная прямая к $\omega$ в точке $P$ пересекает продолжения прямых $AB$ и $AC$ в точках $K$ и $L$ соответственно. Докажите, что $\angle{KOL} > 90^\circ$.
комментарий/решение(1)

---

Задача №5.  a) Существуют ли 5 окружностей на плоскости таких, что каждая окружность проходит через центры в точности трех других окружностей?
b) Существуют ли 6 окружностей на плоскости таких, что каждая окружность проходит через центры в точности трех других окружностей?
комментарий/решение(1)

---