Математикадан облыстық олимпиада, 1999-2000 оқу жылы, 9 сынып
Полные решения этих задач опубликованы в книге, доступный для заказа по ссылке
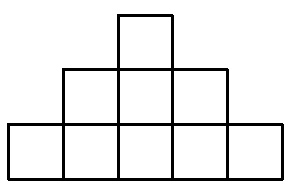
Есеп №1. $p$-ның қандай мәндерінде $p\times p$ квадрат тақтасын бір-бірімен қиылыспайтындай етіп келесі түрдегі фигурамен толықтай жауып шығуға болады?
комментарий/решение(3)
комментарий/решение(3)
Есеп №2. Тақтада үш бүтін сан жазылған. Әр қадамда олардың біреуі сүртіледі де, оның орнына қалған екеуінің қосындысынан 1-ге кем сан жазылады. Осындай біреше қадамнан кейін тақтада қалған сандар 17, 75, 91 сандары. Басында тақтада сына сандар жазылуы мүмкін бе?
а) 2, 2, 2?
б) 3, 3, 3?
комментарий/решение(1)
а) 2, 2, 2?
б) 3, 3, 3?
комментарий/решение(1)
Есеп №3. $\omega $ шеңбері $ABC$ үшбұрышына сырттай сызылған шеңбермен $C$ нүктесінде, ал $AB$ кесіндісімен $K$ нүктесінде жанасады. $CK$ — $C$ бұрышының биссектрисасы екенін дәлелдеңіз.
комментарий/решение(5)
комментарий/решение(5)
Есеп №4. Келесі теңдікті дәлелдеңіз: $\dfrac{\left( {{1}^{4}}+\dfrac{1}{4} \right)\left( {{3}^{4}}+\dfrac{1}{4} \right)\left( {{5}^{4}}+\dfrac{1}{4} \right)\ldots \left( {{11}^{4}}+\dfrac{1}{4} \right)}{\left( {{2}^{4}}+\dfrac{1}{4} \right)\left( {{4}^{4}}+\dfrac{1}{4} \right)\left( {{6}^{4}}+\dfrac{1}{4} \right)\ldots \left( {{12}^{4}}+\dfrac{1}{4} \right)}=\dfrac{1}{313}.$
комментарий/решение(1)
комментарий/решение(1)
Есеп №5. Келесі теңдеуді бүтін сандар жиынында шешіңіздер: ${{\left( x+1 \right)}^{4}}-{{\left( x-1 \right)}^{4}}={{y}^{3}}$.
комментарий/решение(2)
комментарий/решение(2)
Есеп №6. $1999\times 1999$ өлшемді тақтаның бірнеше $1\times 1$ квадраттары, кез-келген баған мен кез-келген қатарда дәл бір боялған шаршы болатындай етіп боялған. Осы тақтадағы кез-келген $1000\times 1000$ квадратында ең болмағанда бір боялған шаршы табылатынын дәлелдеңіз.
комментарий/решение(1)
комментарий/решение(1)
Есеп №7. Қосындысы 1-ге тең теріс емес нақты $a,b$ және $c$ сандары үшін $\dfrac{{{a}^{3}}}{{{a}^{2}}+{{b}^{2}}}+\dfrac{{{b}^{3}}}{{{b}^{2}}+{{c}^{2}}}+\dfrac{{{c}^{3}}}{{{c}^{2}}+{{a}^{2}}}\ge \dfrac{1}{2}$ теңсіздігін дәлелдеңіз.
комментарий/решение(2)
комментарий/решение(2)
Есеп №8. $ABC$ теңбүйірлі үшбұрышында $AB=BC$ және $\angle ABC=120{}^\circ +\alpha $. $AB$ қабырғасына сырттай $ADB$ теңбүйірлі ($AD=DB$) үшбұрышы салынған және $\angle ADB=\alpha $. $DCB$ бұрышын табыңыз.
комментарий/решение(1)
комментарий/решение(1)