Математикадан республикалық олимпиада, 2013-2014 оқу жылы, 9 сынып

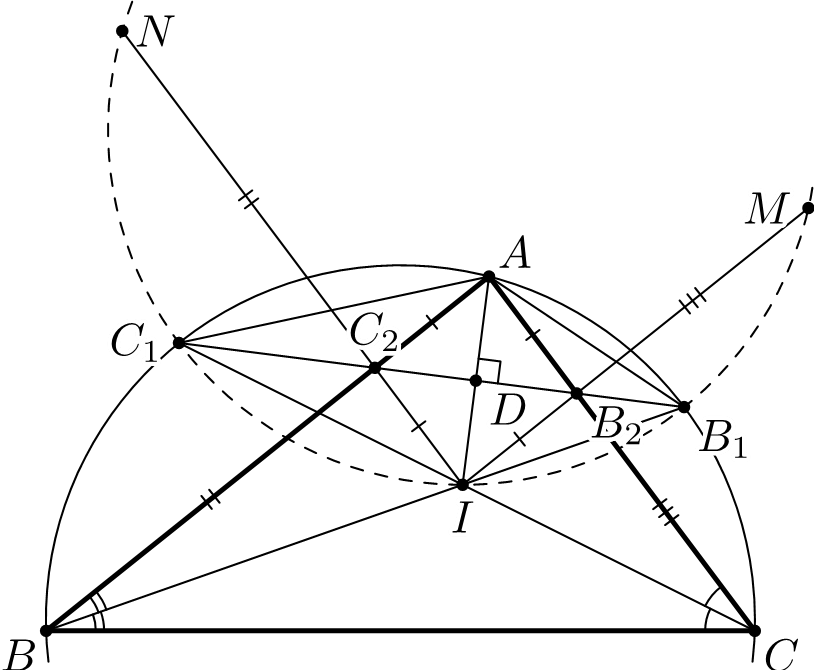
$ABC$ үшбұрышында $I$ нүктесі — оған іштей сызылған шеңбер центрі, ал $\omega$ — оған сырттай сызылған шеңбер. $BI$ және $CI$ түзулері $\omega$-ны сәйкесінше ${{B}_{1}}$ және ${{C}_{1}}$ нүктелерінде, ал $B_1C_1$ түзуі $AB$ және $AC$ түзулерін сәйкесінше $C_2$ және $B_2$ нүктелерінде қияды. $\omega_1$ — $I{{B}_{1}}{{C}_{1}}$ үшбұрышына сырттай сызылған шеңбер болсын. $IB_2$ және $IC_2$ түзулері $\omega_1$-ді сәйкесінше $M$ және $N$ нүктелерінде қисын. Олай болса $B{{C}_{2}}\cdot {{B}_{2}}C={{B}_{2}}M \cdot {{C}_{2}}N$ теңдігін дәлелдеңдер. ( Шалгымбай Б. )

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Поскольку $BB_1$ и $CC_1$ делят углы $B$ и $C$ пополам, то $\angle AC_1B_1 = \angle B_1C_1I = \angle B/2$ и $\angle AB_1C_1 = \angle C_1B_1I = \angle C/2$, откуда $\triangle AC_1B_1 = \triangle IC_1B_1$ (по стороне и двум прилежащим углам), т.е. точки $A$ и $I$ симметричны друг другу относительно прямой или, другими словами, $B_1C_1$ — серединный перпендикуляр отрезка $AI$.