Районная олимпиада, 2014-2015 учебный год, 11 класс


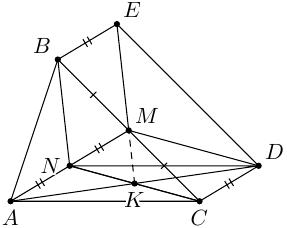
В треугольнике $ABC$ точка $M$ — середина стороны $BC$. Параллелограмм $BCDE$ построен вне треугольника $ABC$ так, что $BE\parallel AM$ и $BE=\dfrac{1}{2}AM$. Докажите, что прямая $EM$ делит пополам отрезок $AD$.
посмотреть в олимпиаде

Комментарий/решение:

Комментарии от администратора Комментарии от администратора №1.     Решение. По признаку параллелограмма, если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Пусть $N$ — середина $AM$, $K$ — точка пересечения отрезков $AD$ и $CN$. Тогда $AN=CD$ и $AN \parallel CD$, откуда $ANDC$ — параллелограмм. Поэтому $K$ — середина отрезков $AD$ и $CN$. Как видим, $KM$ — средняя линия треугольника $BCN$, поэтому $KM \parallel BN$. Также $BN \parallel EM$, так как $BE=NM$ и $BE \parallel NM$. Следовательно, точки $E,M,K$ лежат на одной прямой и $K$ — середина $AD$.