Республиканская олимпиада по математике, 2015 год, 9 класс

Вписанная и вневписанная окружности прямоугольного треугольника $ABC$, в котором угол $C$ прямой, касаются стороны $BC$ в точках $A_1$ и $A_2$ соответственно. Аналогично определим точки ${{B}_{1}}$ и ${{B}_{2}}$. Докажите, что отрезки ${{A}_{1}}{{B}_{2}}$ и ${{B}_{1}}{{A}_{2}}$ пересекаются на высоте проведённой из вершины $C$ треугольника $ABC$. ( М. Кунгожин )

Комментарий/решение

Положим что прямые $B_{2}A_{1}$ и высота $CH$ пересекаются,в точке $X$. Тогда

$\dfrac{XA_{1}}{cos \angle B}=\dfrac{CA_{1}}{sin( \angle B+ \angle B_{2} )}; \dfrac{XB_{2}}{sin \angle B}=\dfrac{CB_{2}}{sin(\angle B+ \angle B_{2})}$

Откуда $ \dfrac{XA_{1}}{XB_{2}}=\dfrac{CA_{1}}{CB_{2}}*ctg \angle B$

По теореме Менелая , рассмотрев треугольник $\Delta A_{1}A_{2}B_{2}$ , получим

$\dfrac{A_{2}O}{B_{2}O}=(1+\dfrac{A_{1}A_{2}}{CA_{1}})*\dfrac{CA_{1}}{CB_{2}}*ctg \angle B$

$O$ - точка пересечения высоты и $B_{2}A_{2}$

Учитывая теорему Чевы в треугольнике $\Delta CA_{2}B_{2}$ , если отрезки $A_{1}B_{2};B_{1}A_{2};CH$ действительно пересекаются в одной точке , то должно выполнятся соотношение $\dfrac{A_{1}A_{2}}{CA_{1}}*\frac{CA_{1}}{B_{1}B_{2}} * \dfrac{B_{2}O}{A_{2}O}=1$ .

Получим $\dfrac{A_{1}A_{2}*CB_{2}*tg \angle B}{B_{1}B_{2}*CA_{2}}=1$ или

$AC*A_{1}A_{2}*CB_{2}=BC*B_{1}B_{2}*CA_{2}$ , докажем теперь это , условие можно переписать через радиус вневписанных окружностей , и вписанной

$AC*(R_{BC}-r_{ABC})*R_{AC}=BC*(R_{AC}-r_{ABC})*R_{BC}$

По формуле радиусы вневписанных окружностей, равны $R_{BC}=\dfrac{S}{p-BC}$ и $R_{AC}=\dfrac{S}{p-AC}$ ; $r_{ABC}=\dfrac{AB+AC-BC}{2}$ , подставляя это в условие получаем тождество , значит выше сказанное условие выполняется, ч.т.д

Решение. Обозначим точку пересечения $A_2 B_1$ через $X$ и покажем, что $CX=CB_1=r$, что докажет требуемое. $\triangle A_2 JC \sim \triangle B_1 IC=>\frac {CJ} {CI}=\frac {CA_2} {CB_1} =>\triangle CIJ \sim \triangle CB_1 A_2=>A_2 JCD$ – вписанный. Значит, $CD⊥AJ$ и $∠CDB_1=45°$. Тогда $∠XB_1 C=\frac {∠A} 2+45°,∠B_1 XC=180°-(90°-∠A)-∠XB_1 C=\frac {∠A} 2+45°$, ч.т.д.

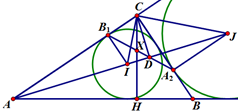
Пусть $I$ центр вписанной окружности. Заметим что  $IB_1A_1C$- квадрат и $B_2C=B_1A , CA_2=A_1B$. Отсюда легко заметить что $\triangle IA_1B= \triangle B_1CA_2$ и $\triangle IB_1A=\triangle A_1CB_2$. легко увидеть что $B_1A_2//IB$ и $B_2A_1//AI$ . Пусть $X=B_1A_2 \cap B_2A_1$ $\angle B_1XA_1=\angle B_2XA_2=\angle AIB=145$. Так как $\angle B_1XA_1=145$ и $\angle B_1CA_1=90$ легко увидеть что $C$ центр описанной окружности $\triangle B_1XA_1$ дальше по счету углов получаем что $\angle ABC= \angle ACX$ значит $CX$ высота $\triangle ABC$.

бро разве не 135?

Ведем обозначение $AB=c, BC=a, AC=b, p=\frac{a+b+c}{2},A_1B_2 \cap A_2B_1=X, A_2B_2 \cap CX=Z, CX \cap AB=Y$

По теореме чевы для $A_2B_2C$:

$\frac{B_2B_1}{B_1C}*\frac{CA_1}{A_1A_2}*\frac{A_2Z}{B_2Z}=1$

По Ratio lemma:

$\frac{A_2Z}{B_2Z}=\frac{sin BCY}{sin ACY}*\frac{CA_2}{CB_2}$=>>тк $CA_1=B_1C$ =>> $\frac{sin ACY}{sin BCY}=\frac{B_1B_2}{A_1A_2}*\frac{CA_2}{CB_2}$

Заметим что достаточно доказать что

$\frac{B_1B_2}{A_1A_2}*\frac{CA_2}{CB_2}=\frac{AC}{BC}$

Заметим что $CA_2=p-b, CB_2=p-a, B_1B_2=c-a, A_1A_2=c-b$ значит

$\frac{B_1B_2}{A_1A_2}*\frac{CA_2}{CB_2}=\frac{AC}{BC}$ <=> $\frac{b}{a}=\frac{c-a}{c-b}*\frac{p-b}{p-a}$

Умножив все можно получить что надо доказать:

$c^2a-a^3+a^2b=c^2b-b^3+ab^2$

По теореме пифагора $c^2=a^2+b^2$ подставляем

И получаем $a^3+ab^2-a^3+a^2b=b^3-b^3+ab^2+a^2b$

Пусть $B_1A_2$ и $B_2A_1$ пресекаются в $X$ и $CA_1=CB_1=AB_2=BA_2=c$ и $AB_1=a;\;A_1B=b$ тогда $CA_2=b$ и $CB_2=a$ $\Rightarrow$ $B_1A_2=\sqrt{b^2+c^2}$ $\Rightarrow$ $B_2A_2=\sqrt{a^2+b^2}$ также $\sin(A_2B_1C)=\sin(A_2B_1B_2)=\dfrac{b}{\sqrt{b^2+c^2}}$ $\Rightarrow$ из $\sin(B_2A_2B_1)= \dfrac{b}{\sqrt{b^2+c^2}} × \dfrac{a-c}{\sqrt{a^2+b^2}}$ также $\sin(B_1A_2C)=\dfrac{c}{\sqrt{b^2+a^2}}$ $\Rightarrow$ Из Ratio Lemma в $A_1B_2A_2\Rightarrow\dfrac{B_2X}{XA_1}= \dfrac{\sqrt{a^2+b^2}}{b-c}\times \dfrac{ b(a-c)}{\sqrt{a^2+b^2}}\times \dfrac{1}{\sqrt{b^2+c^2}}\times \dfrac{\sqrt{b^2+c^2}}{c} = \dfrac{b(a-c)}{c(b-c)}$

Теперь пересекаем $B_2A_1$ с высотой в точке $X_1\Rightarrow \dfrac{B_2X_1}{X_1A_1}= \dfrac{a}{c}\times \dfrac{\cos A}{\cos B}$

\[\cos A = \frac{(a+c)^2+(a+b)^2-(b+c)^2}{2(a+b)(a+c)}\]

Аналогично опрелелим $\cos B$ через $a;b;c$ тогда

\[\dfrac{B_2X_1}{X_1A_1}= \frac{a}{c}\times \frac{(a^2+ac+ab-bc)(b+c)}{(b^2+ab+bc-ac)(a+c)} = S\]

На этом этапе Б.О.О заменим:

$a=1;\;c=\tan(a);\;b=\tan(a)\times\tan(45+a)$ и возьмем $t=\tan(a)\Rightarrow c=t;\;b=t\frac{1+t}{1-t}$

\[a^2+ac+ab-bc = 1+t+t\frac{1+t}{1-t}-t^2\frac{1+t}{1-t} = t\frac{1-t^2}{1-t} + 1 + t = t^2+2t+1=(t+1)^2\]

\[b+c = t\frac{1+t}{1-t} + t = \frac{2t}{1-t}\]

\[b^2+ab+bc-ac = \frac{4t^2}{(1-t)^2}\]

\[a+c = t+1\]

\[S = \frac{(t+1)^2\times \frac{2t}{1-t}}{\frac{4t^2}{1-t} \times (t+1)\times t} = \frac{(t+1)(1-t)}{2t^2}= \frac{B_2X_1}{X_1A_1}\]

\[\frac{B_2X}{XA_1} = \frac{b(a-c)}{c(b-c)} = \frac{t(t+1)(1-t)}{t\big(t(t+1)-t(1-t)\big)} = \frac{(t+1)(1-t)}{2t^2}\]

\(\Rightarrow B_2X_1/X_1A_1=B_2X/XA_1 \Rightarrow X_1=X\) ч.т.д