Математикадан республикалық олимпиада, 2016-2017 оқу жылы, 9 сынып


$ABC$ үшбұрышының қабырғаларына үшбұрыштың сырт жағына қарай аудандары өзара тең болатын $ABLK$, $BCNM$ және $CAQP$ тіктөртбұрыштары салынған. $X$, $Y$ және $Z$ нүктелері сәйкесінше $KQ$, $LM$ және $NP$ кесінділерінің орталары. $AX$, $BY$ және $CZ$ түзулерінің бір нүктеде қиылысатынын дәлелдеңіздер. ( М. Кунгожин )
посмотреть в олимпиаде

Комментарий/решение:

Комментарии от администратора Комментарии от администратора №1.     Решение. Пусть стороны треугольника $ABC$ имеют фиксированные стороны. Заметим, что если не фиксированные стороны прямоугольников увеличивать пропорционально, то прямые $AX,BY$ и $CZ$ будут постоянными. Следовательно, эти прямые проходят через какую-то фиксированную точку треугольника. Пусть точка $O$ — центр описанной окружности треугольника $ABC$. Докажем, что $O$ — искомая точка.

Обозначим $D=CP \cap BL$. Тогда точки $A,B,C,D$ лежат на одной окружности с диаметром $AD$; также на этом диаметре лежит точка $O$. Пусть $X_1=AD \cap KQ$. Так как $\angle CAD = \angle CBD$ и $$\angle CAD + \angle QAX_1= \angle CBD + \angle ABC = 90^\circ,$$ то $\angle QAX_1=\angle ABC$. Аналогично, $\angle KAX_1 = \angle ACB$. Пусть прямоугольники имеют площадь $S$. Тогда, $$\frac{QX_1}{KX_1}=\frac{AQ}{AK} \cdot \frac{\sin QAX_1}{\sin KAX_1} = \frac{S/AC}{S/AB} \cdot \frac{\sin ABC}{\sin ACB} =\frac{AB}{AC} \cdot \frac{AC}{AB}=1,$$ то есть $X_1$ — середина отрезка $QK$ или $X_1$ совпадает с $X$. Следовательно, прямая $AX$ проходит через точку $O$. Аналогичное утверждение можно доказать для прямых $BY$ и $CZ$.

  1
2024-09-23 19:45:45.0 #

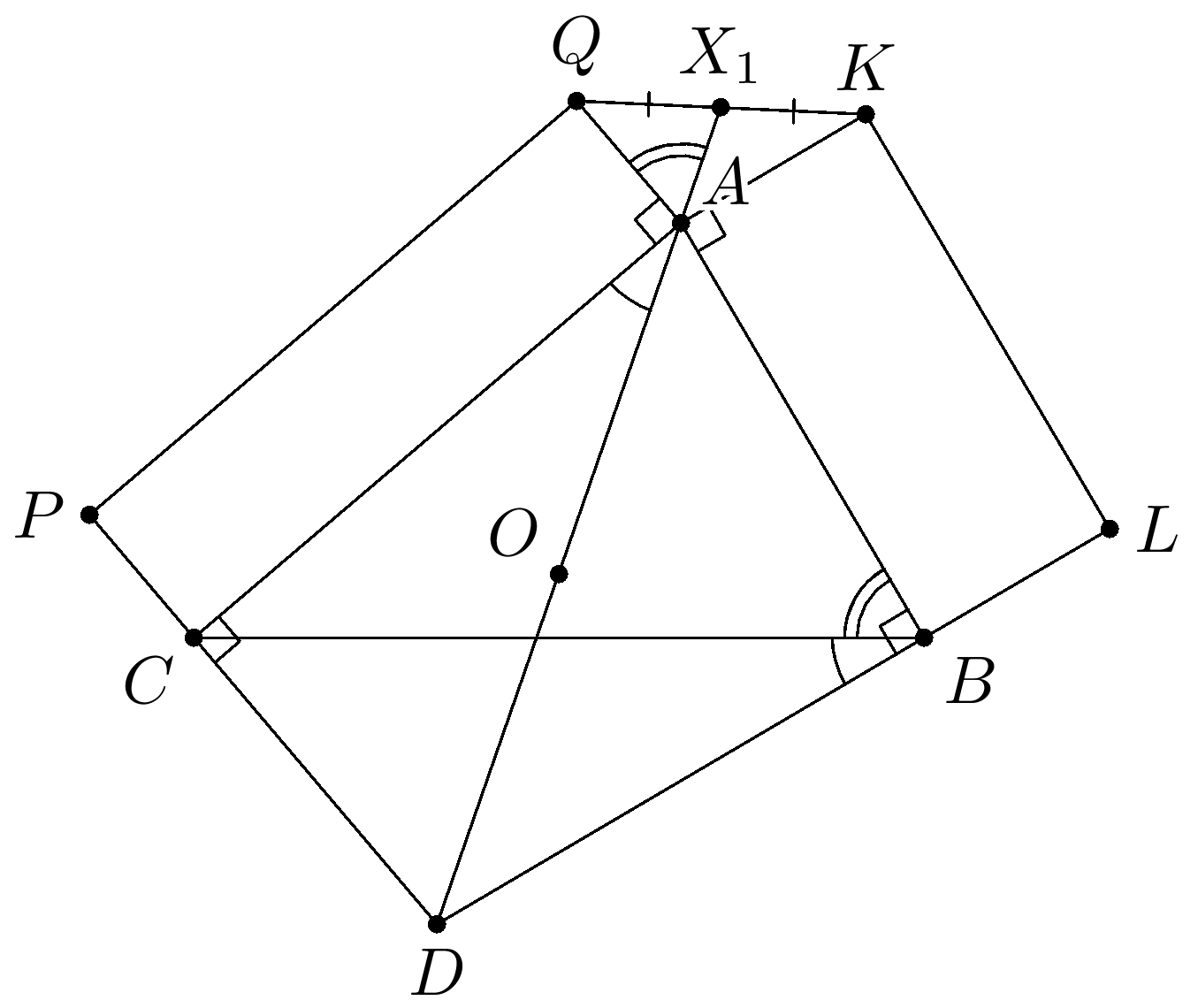
Лемма:

На сторонах $AB,AC$ треугольника $ABC$ построены квадраты $ABPX$ и $ACQY$. Тогда верно, что высота $\triangle ABC$ в точке $A$ является медианой $\triangle AXY$.

Построим из задачи прямоугольники с площадью $S=AB\cdot AC$. Тогда верно, что $ACPQ$ и $ABLK$ отличаются поворотом. Треугольник из леммы отличается от треугольника $AKQ$ симметрией относительно общей биссектрисы $\angle BAC$ и $\angle QAK$. Поэтому $AX$ - изогональ к высоте $\triangle ABC$ в точке $A$. Поэтому задача решена, так как линейное движение точек прямоугольника линейно передвигает и точки $X,Y,Z$.

ImaRHB
  1
2026-01-16 13:29:36.0 #

Пусть $AB = c; AC = b; BC = a.$

И так же $BM = CN = 1; CP = AQ = y; AK = BL = x.$

И пусть угол $LBM = Y;$ угол $KAQ = X;$ угол $NCP = Z.$

В треугольнике $LBM$:

\[\cos LBY = \frac{3x^2 + 6 x \cos X - 1}{8 x t}, \quad \text{где } t = BY\]

\[\cos LBM = \frac{-x^2 + 6 x \cos X + 3}{8 t} \tag{1}\]

\[\frac{\cos LBY}{\cos LBM} = \frac{1}{x} \cdot \frac{3x^2 + 6 x \cos X - 1}{-x^2 + 6 x \cos X + 3}\]

Аналогично выражаем:

\[\frac{\cos NCZ}{\cos ZCP} = \frac{-y^2 + 6 y \cos Y + 3}{3 y^2 + 6 y \cos Y - 1} \cdot y \tag{2}\]

\[\frac{\cos XAQ}{\cos XAK} = \frac{3 y^2 + 6 x y \cos Z - x^2}{3 x^2 + 6 x y \cos Z - y^2} \tag{3}\]

Теперь вспомним, что $x = a/c; y = a/b$

также $\cos X = -\cos ABC = -\frac{c^2 + a^2 - b^2}{2 c a}$

и аналогично заменяем остальные косинусы, и получится:

\[(1) = \frac{4 a^2 - 3 c^2}{4 b^2 - 3 c^2}, \quad\]

\[(2) = \frac{4 c^2 - 3 b^2}{4 a^2 - 3 b^2}, \quad\]

\[(3) = \frac{4 b^2 - 3 a^2}{4 c^2 - 3 a^2}\]

Умножив и раскрыв скобки, поймем что это 1:

\[\frac{\cos LBY}{\cos LBM} \cdot \frac{\cos NCZ}{\cos ZCP} \cdot \frac{\cos XAQ}{\cos XAK} = 1\]

Следовательно из триг чевы вызодит условие

slverg