2-я международная Иранская олимпиада по геометрии, 2015 год, вторая лига, 9-10 классы

На рисунке ниже точки $P, A, B$ лежат на окружности, а точка $Q$ внутри окружности так, что $\angle{PAQ}=90^\circ$ и $PQ=BQ$. Докажите, что значение разности углов $\angle{AQB}-\angle{PQA}$ равна центральному углу, опирающемуся на дугу $AB$.

Комментарий/решение

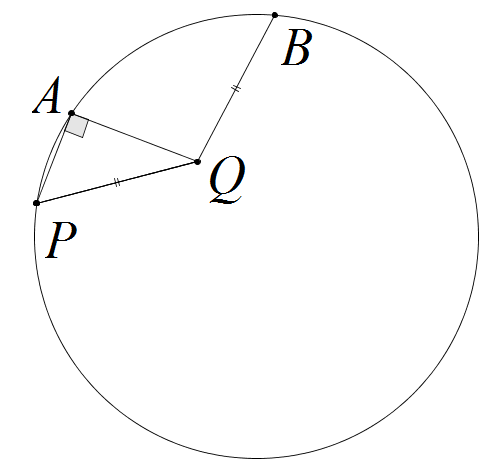
Пусть O - центр окружности, а X - точка на прямой AP за точку A, такая что $\angle PQA = \angle AQX$ $\Rightarrow$ $$\angle AQB - \angle PQA = \angle AQB - \angle AQX = \angle XQB$$

$\angle BPQ = 90^\circ - (\frac{\angle XQB}{2} + \angle PQA)$ $\Rightarrow$ $\angle BPA = \angle QPA - \angle BPQ = 90^\circ - \angle PQA - 90^\circ + \frac{\angle XQB}{2} + \angle PQA = \frac{\angle XQB}{2} = \frac{\angle AOB}{2}$ $\Rightarrow$

$$\angle AQB - \angle PQA = \angle XQB = \angle AOB$$

Пусть <BQA=a, а <AQP=b и <BOA=alfa и нам надо доказать что a-b=alfa(!)

<QPA=90-b

<QPB=(180-a-b)/2

<BPA= <QPA - <QPB= 90-b- (180-a-b)/2 = 0.5a- 0.5b=<BPA.

Дуга AB=2×<BPA=2×(0.5a-0.5b)= a-b.

Дуга AB= <BOA= alfa= a-b что и требовалось доказать!

О- центр окружности

BQA=2a , PQA=2b

BPQ=90-a-b , APQ=90-2b => APB=a-b => AOB=2a-2b

(О-центр описанной окружности треугольника АBP)

Пусть $\omega-$ данная окружность с центром $O$,$AQ\cap \omega=A,S.OQ\cap\overset\frown{PAB}=R,\angle RPS=\alpha,\angle ASP=\beta$.$\triangle PQO=\triangle BQO\Rightarrow \angle PQR=\angle BQR\Rightarrow \triangle PQR=\triangle BQR\Rightarrow \angle SPR=\angle PRO=\angle BRO=\alpha,\angle BOR=180^\circ-2\alpha.\angle ARO=\angle ARP+\angle PRO=\alpha+\beta.\angle AOR=180^\circ-2\alpha-2\beta\Rightarrow \angle AOB=360^\circ-4\alpha-2\beta.\angle RAS=\angle RPS=\alpha.\angle AQR=180^\circ-2\alpha-\beta$.$\angle AQB-\angle PQA=\angle BQR+\angle AQR-\angle PQR+\angle AQR=2\angle AQR=2(180^\circ-2\alpha-\beta)=\angle AOB$