Республиканская олимпиада по физике 2012, 10 класс, теоретический тур

Катастрофы (8 баллов)
Часть А. Цунами (3 балла)
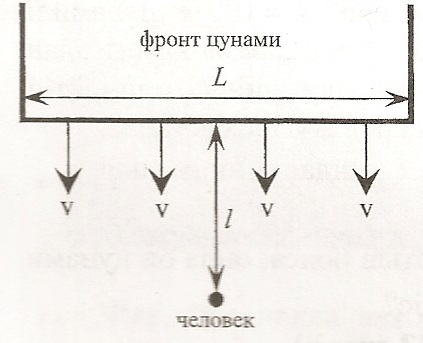
Человек, находящийся на суше, замечает цунами, которое приближается к нему со скоростью $\vartheta= 25$ км/ч и имеет ширину $L= 100$ м. Человек находится прямо напротив середины фронта цунами на расстоянии $l=50$ м от него. Чтобы спастись, он начинает бежать с некоторой постоянной скоростью в неизменном направлении.
1. С какой минимальной скоростью $u_{\min}$ должен бежать человек, чтобы не попасть под цунами?
2. Под каким углом к фронту цунами должен двигаться человек, если он двигается со скоростью $u_{\min}$?

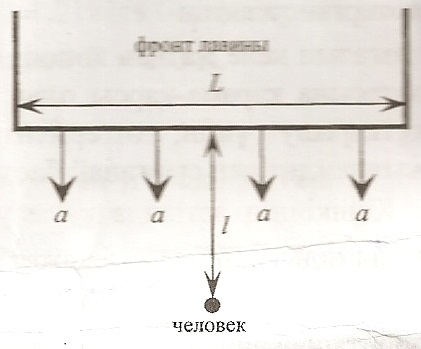
Часть В. Лавина (3 балла) Человек катается на лыжах по склону горы, которую можно считать наклонной плоскостью. В некоторый момент времени он замечает, что сверху срывается лавина шириной $L=100$ м, движущаяся с постоянным ускорением $a=5,0$ м/с$^2$. Человек находится прямо напротив середины фронта лавины на расстоянии $l=100$ м от нее. Чтобы спастись, он начинает ехать с некоторой постоянной скоростью в неизменном направлении.
1. С какой минимальной скоростью $u_{\min}$ должен ехать человек, чтобы не попасть под лавину?
2. Под каким углом к фронту лавины должен двигаться человек, если он двигается со скоростью $u_{\min}$?

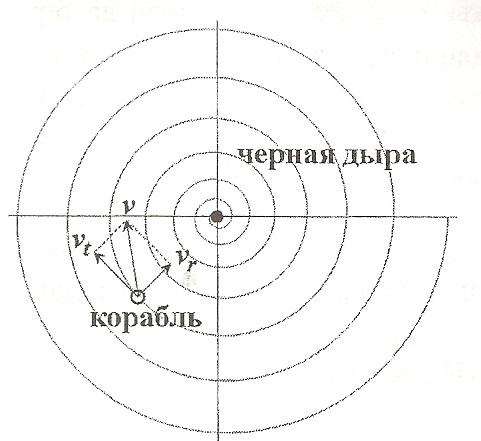
Часть С. Черная дыра (2 балла) Космический корабль попадает в черную дыру и начинает падать на нее с начального расстояния $R$ по спирали таким образом, что его радиальная $\vartheta_{r}$ и тангенциальная $\vartheta_{t}$, скорости зависят от расстояния $r$ до центра черной дыры по закону: $\vartheta_{r}=\alpha/r$ и $\vartheta_{t}=\beta r^{2}$, где $\alpha$ и $\beta$ — некоторые известные постоянные величины. Радиальная скорость — это компонента вектора скорости $\vartheta$, направленная к центру черной дыры, а тангенциальная скорость — это компонента , перпендикулярная радиальной.
1. Какой угол составляет вектор скорости $\vartheta$ с направлением на центр черной дыры в момент времени, когда расстояние до центра черной дыры сократилось вдвое и стало равным $R/2$?
2. Сколько времени прошло от начала падения до этого момента времени?

Комментарий/решение

Часть A:

Запишем координаты человека $(x_1;y_1)$ и для цунами $(y_2)$:

$x_1=ut\sin \theta=\frac{L}{2}$

$y_1=ut\cos \theta$

$y_2=l-\vartheta t$

В момент столкновения:

$y_1=y_2\rightarrow l=(\vartheta+u\cos \theta)t$

Использую их можно получить что:

$u=\frac{\vartheta}{\frac{2l}{L}\sin \theta - \cos \theta}$

Возьмем производную знаменателя как $0$ чтобы выразить $u_{min}$:

$\frac{2l}{L}\cos \theta + \sin \theta=0 \rightarrow \tan \theta = -\frac{2l}{L}$

$\theta=\arctan(-\frac{2l}{L})=45^\circ$

Значит что:

$u_{min}\approx 17.7$ км/ч

Часть B:

В случае когда лавина ускоряется:

$y_2=l-\frac{at^2}{2}$

$y_1=y_2\rightarrow l=ut\cos \theta + \frac{at^2}{2}$

$t=\frac{L}{2u\sin \theta}$

$l=\frac{L\cot \theta}{2}+\frac{aL^2}{8(u\sin \theta)^2}$

Аналогично части A возьмем производную как 0:

$-\frac{L}{2\sin^2 \theta}-\frac{aL^2\cos \theta}{4u^2(\sin \theta)^3}=0$

$\tan \theta=-\frac{aL}{2u^2}$

$l=-\frac{u^2}{a}+\frac{aL^2(aL^2+4u^4)}{8u^2a^2L^2}$

$\frac{u^4}{2a}+lu^2-\frac{aL^2}{8}=0$

По легкому дискриминанту находим:

$u_{min}=\sqrt{al(-1+\sqrt{1+(\frac{L}{2l})^2})}\approx 7.7$ м/с

И окончательно найдем угол:

$\theta=\arctan(-\frac{aL}{2u^2}) \approx 13.3^\circ$

Часть C:

C1:

$\tan \alpha=\frac{\vartheta_{t}}{\vartheta_{r}}$

Когда корабль опускается на $r=\frac{R}{2}$:

$\vartheta_{t}=\frac{\beta R^2}{4}$

$\vartheta_{r}=\frac{2\alpha}{R}$

Из этого получаем:

$\tan \alpha=\frac{\beta R^3}{8\alpha}$

C2:

$\frac{dr}{dt}=-\vartheta_{r}=-\frac{\alpha}{r}$

$\int_{R}^{\frac{R}{2}} r dr = -\alpha \int_{o}^{T} dt$

$\alpha T=\frac{3R^2}{8} \rightarrow T=\frac{3R^2}{8\alpha}$