Областная олимпиада по физике 2021, 11 класс, теоретический тур
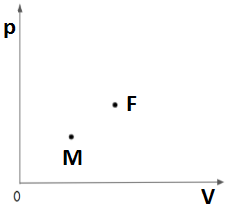
[6 баллов]. Среди трудов Уильяма Томсона нашли манускрипт с $pV$-диаграммой для идеального газа. На диаграмме был нарисован циклический процесс в виде треугольника $KLM$, где угол при вершине $M$ был прямым. Точка $F$ изображенная на рисунке лежит на середине стороны $KL$. В данной точке, теплоемкость многоатомного газа равно нулю. Зная только точки $M$ и $F$ восстановите данный цикл. Объем в точке $K$ меньше чем в $L$. (Можно использовать только циркуль и линейку без делений).
посмотреть в олимпиаде
Комментарий/решение:
Для восстановления цикла, описанного в манускрипте Уильяма Томсона (Лорда Кельвина), нам необходимо проанализировать условие, при котором теплоемкость идеального газа обращается в нуль.
1. Условие нулевой теплоемкости
Теплоемкость \bm{C = 0} в процессе означает, что процесс в данной точке является адиабатическим. Для идеального газа уравнение адиабаты в осях \bm{(P, V)} в дифференциальной форме выглядит так:

Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.