Юниорская олимпиада по математике. Заключительный этап. 2020-2021 учебный год. 8 класс.
Жазықтықта 16 нүкте суретте көрсетiлгендей орналасқан. Төбелерi осы нүктелерде болатын неше үшбұрыш бар?
A) 326 B) 516 C) 44 D) 560 E) 246
посмотреть в олимпиаде
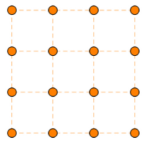
A) 326 B) 516 C) 44 D) 560 E) 246
Комментарий/решение:
Алдымен $3$ нүктенің бір сызықта кездесетін жағдайларды санап шығайық. $4$ нүктеден $3$ нүктені $\left ( \dfrac{4}{3} \right )$ = $\dfrac{4!}{3!} = 4$.
Бізде $4$ тік, $4$ көлденен $16$ нүкте бар. Және үш нүктені бір қатарда жататындай қылып $3 \times3$ шаршыда диоганалін тандасақ болады, бізде $4$ $3 \times3$ шаршы бар, және $4 \times 4 $ шаршыда екі диоганлі бар. Демек барлығы $4 \cdot 4 + 4 \cdot 4 + 4 \cdot 1 + 2 \cdot 4 = 44$
Біз $16$ нүктеден $3$ нүктені $\left ( \dfrac {16}{3} \right ) = \dfrac{16!}{13! \cdot 3!}$ $=560$, және жаңағы $44$ бір сызықта жататын жағдайларды азайтамыз $560 - 44 = 514$.
Жауабы $:C)$

Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.