11-я международная Иранская олимпиада по геометрии, 2023 год, третья лига, 11-12 классы

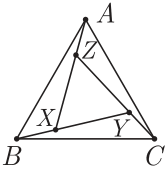
На рисунке ниже равносторонний треугольник $ABC$ разделён на 4 треугольника равных площадей; три из них — это равные треугольники $ABX$, $BCY$, $CAZ$, а четвёртый, меньший, — это равносторонний треугольник $XYZ$. Докажите, что точки $X, Y, Z$ лежат на вписанной окружности треугольника $ABC$.

Комментарий/решение

Пусть точки $X,Y,Z$ лежат на вписанной окружности, тогда покажем что $S_{ABX}=S_{BCY}=S_{CAZ}=S_{XYZ}$

Доказательство : из условия $AZ=BX=CY=a$ и $XY=b$ тогда по теореме косинусов например для $AZC$ где $AZC=120^{\circ}$ получается $a^2+(a+b)^2+a(a+b)=AC^2$ но по теореме о секущей и касательной $\dfrac{AC^2}{4}=a(a+b)$ тогда $a^2+(a+b)^2+a(a+b)=4a(a+b)$ или $b^2=a^2+ab \ (1)$ но $S_{AZC}=S_{XYZ}$ это и есть $(1)$ ч т.д