Европейская математическая олимпиада среди девочек (EGMO). 2023 год. Словения

Улитка Турбо сидит в некоторой точке окружности длиной 1. Дана бесконечная последовательность действительных положительных чисел $c_{1}, c_{2}, c_{3}, \ldots$. Турбо последовательно проползает расстояния $c_{1}, c_{2}, c_{3}, \ldots$ по этой окружности, каждый раз выбирая ползти ли ей по часовой стрелке или против часовой стрелки.
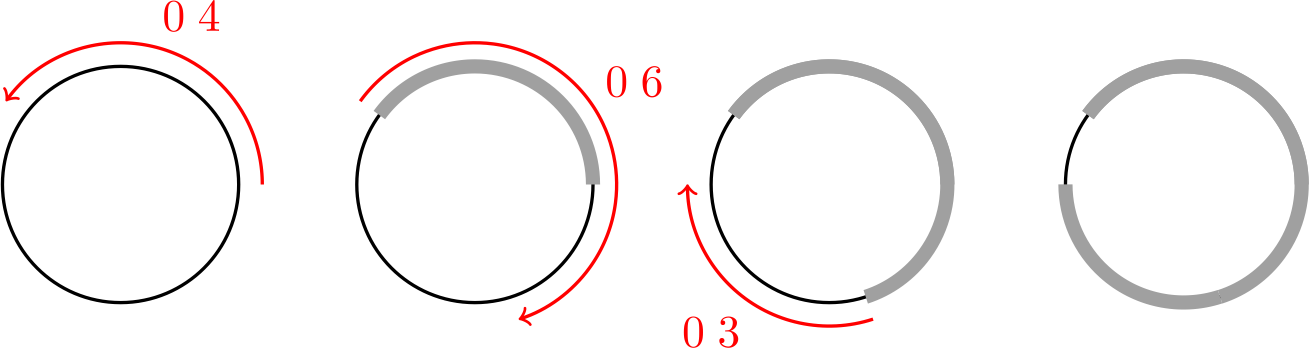
   Например, если последовательность $c_{1}, c_{2}, c_{3}, \ldots$ это $0.4,0.6,0.3, \ldots$, то Турбо может начать ползти следующим образом:

Определите наибольшую константу $C > 0$ со следующим свойством: для любой последовательности действительных положительных чисел $c_{1}, c_{2}, c_{3}, \ldots$ таких, что $c_{i} < C$ для каждого $i$, Турбо может (после изучения последовательности) гарантировать, что на окружности есть точка, которую она никогда не посетит и не переползёт.