Математикадан облыстық олимпиада, 2009-2010 оқу жылы, 10 сынып

$ABCD$ трапециясына іштей сызылған $\omega$ шеңберінің центрі $I$ нүктесі болсын. $AD$ және $BC$ қабырғалары $R$ нүктесінде қиылыссын. $P$ және $Q$ нүктелері $\omega$ шеңберінің сәйкесінше $AB$ және $CD$ қабырғаларымен жанасу нүктелері болсын. $P$ нүктесі арқылы өтетін және $PR$ кесіндісіне перпендикуляр болатын түзу $AI$ және $BI$ түзулерін сәйкесінше $A_0$ және $B_0$ нүктелерінде қияды, ал $Q$ нүктесі арқылы өтіп $QR$ кесіндісіне перпендикуляр болатын түзу $CI$ және $DI$ түзулерін сәйкесінше $C_0$ және $D_0$ нүктелерінде қияды. $A_0D_0=B_0C_0$ екенін дәлелдеңіздер.

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Воспользуемся следующей леммой.
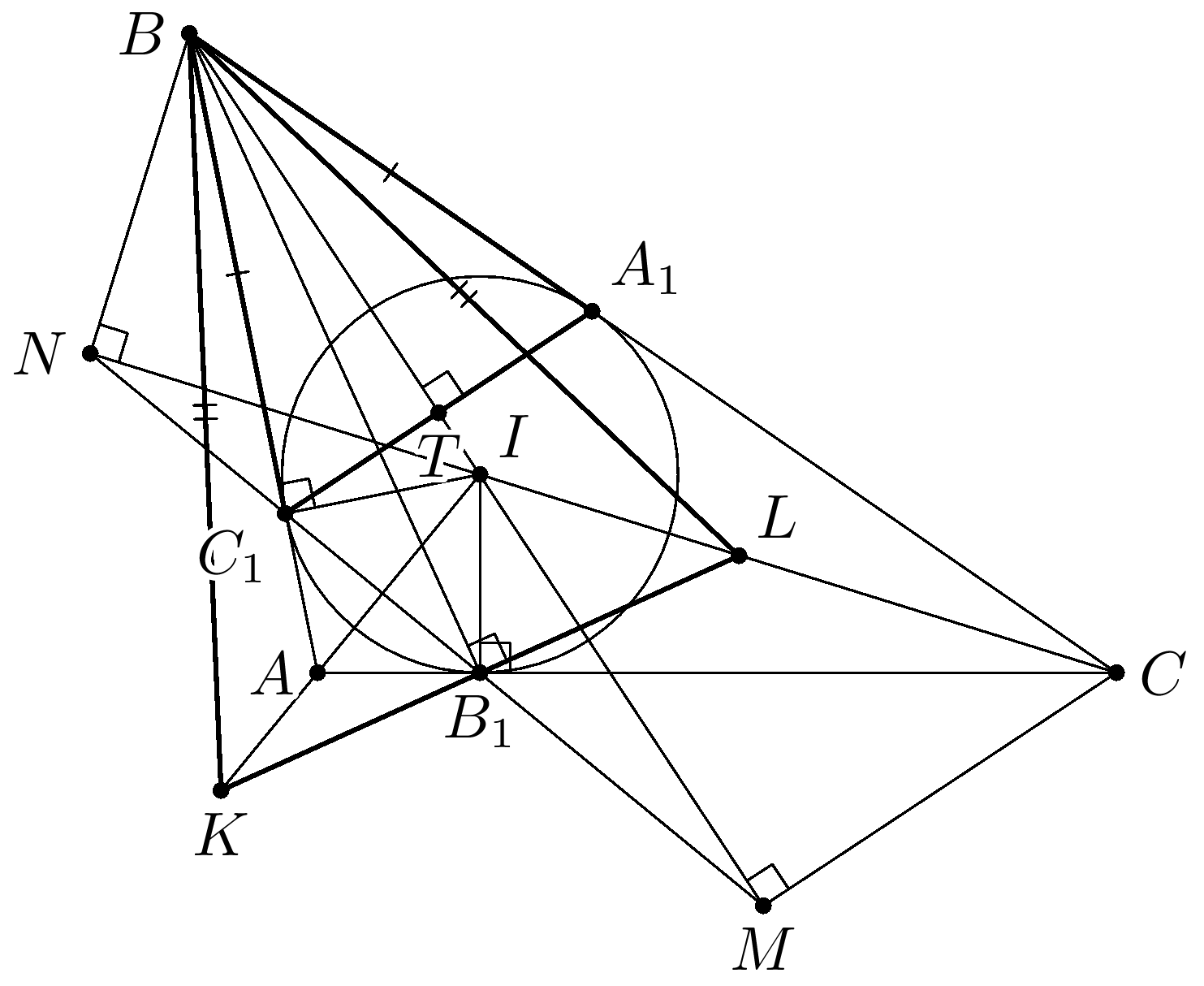
Лемма. В треугольник $ABC$ вписана окружность с центром $I$, которая касается $AC$ в точке $B_1$. Пусть прямая, проходящая через точку $B_1$ и перпендикулярная $BB_1$, пересекает прямые $AI$ и $CI$ соответственно в точках $K$ и $L$. Тогда треугольник $BKL$ равнобедренный и подобен треугольнику $BA_1C_1$.
Доказательство. Пусть вписанная окружность касается сторон $AB$ и $BC$ в точках $C_1 $ и $A_1$ соответственно.
Обозначим $N=B_1C_1 \cap CI$, $M=B_1C_1 \cap BI$, $T=BI \cap C_1A_1$. Пусть $C_1$ лежит на отрезке $B_1N$. Тогда $\angle BIN = \angle B/2+\angle C/2=90^\circ - \angle A/2=\angle AC_1B_1=\angle NC_1B$, то есть точки $B,I,C_1,N$ лежат на одной окружности с диаметром $BI$. Откуда $\angle BNC=90^\circ$. Также можно показать, что $\angle BMC=90^\circ$. Следовательно, каждая из четверок $(B,C,M,N)$, $(B,L,B_1,N)$ лежат на одной окружности. Откуда следует цепочка равенств $\angle LBB_1= \angle LNB_1=\angle CBM=\angle A_1BT$, что дает подобие прямоугольных треугольников $LBB_1$ и $A_1BT$. Аналогично, $\triangle KBB_1 \sim \triangle C_1BT$. Значит, $\triangle BA_1C_1 \sim \triangle BKL$ и так как $BA_1=BC_1$, то $BL=BK$.
Можно заметить, что из использованного метода доказательства, лемма верна и для точки касания вневписанной окружности соответствующей вершине $B$.

Укажите, пожалуйста, автора задачи.

Если бы мы знали. К сожалению многих авторов мы не знаем. В тех материалах, откуда мы взяли, не было указано. Если напишите, будем рады.

Спасибо, а не могли бы вы предоставить решение этой задачи, очень уж она меня заинтересовала.

Постараемся в два-три дня выложить.

Cпасибо большое

Добавили. Спасибо Кунгожину Медеубеку, что уделил время и отправил решение.

Спасибо

Достаточно заметить, что:

В треугольниках $APR$ - $A_0$, $I$

$DRQ$ -$D_0$, $I$

$PBR$ - $B_0$, $I$

$QCR$ - $C_0$, $I$ изогонально сопряжены.Из полученного нетрудно вывести, что $\angle {A_0}RD=\angle PRI=\angle {B_0}RB$. Аналогично $\angle ARD_0=\angle IRQ=\angle BRC_0$. Также $\angle {D_0}RP=\angle QR{B_0}$. Значит $RQ$ - биссектриса $\angle {D_0}R{C_0}$. Учитывая, что $RQ$ перпендикулярна ${D_0}{C_0}$ получаем, что $R{D_0}{C_0}$ равнобедренный, $R{D_0}=R{C_0}$. Аналогично ${A_0}R={B_0}R$. В совокупности с равенствами из изогональной сопряженности это дает нам равенство треугольников ${A_0}RD_0$ и ${B_0}RC_0$, откуда и вытекает требуемое

Можете обьяснить как треугольник KBB1 подобен треугольнику C1BT

нафик тебе обьеснение если ты тупой полибому не понимаеш этот задача