Районная олимпиада, 2025-2026 учебный год, 10 класс

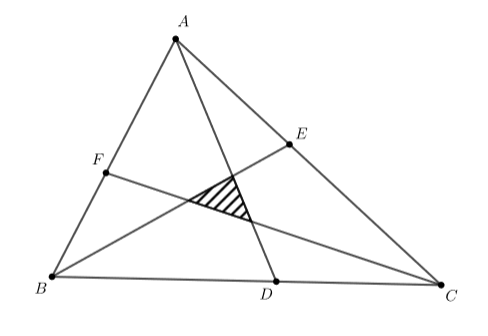
В треугольнике $ABC$ точки $D$, $E$ и $F$ лежат на сторонах $BC$, $CA$ и $AB$ соответственно, так что $BD:DC = CE:EA = AF:FB = 3:2$, как показано на рисунке. Если площадь заштрихованной области равна 100, какова площадь треугольника $ABC$?

Комментарий/решение

Юзаем теорему рауса и получаем ответ 1900

Если что теорема Рауса определяет отношение между площадями заданного треугольника и треугольника, образованного тремя попарно пересекающимися чевианами.

То есть если x,y,z это соотношение в котором AD, BE, CF делит стороны треугольника то площадь заштрихованной области равен

$\frac{(xyz - 1)^2}{(xy + y + 1)(yz + z + 1)(zx + x + 1)}$

От площади исходного треугольника. Так как у нас x=y=z=1,5 то и область заштрихованного треугольника равен 1/19 от исходного