1. Олимпиадалар тізімі
  2. Математика олимпиадалары
  3. Дистанциялық олимпиадалар
  4. Геометриядан Иран олимпиадасы
  5. 11-я олимпиада, 2024 год
  6. Первая лига, 7-8 классы

11-я международная Иранская олимпиада по геометрии, 2024 год, первая лига, 7-8 классы


Есеп №1.  $4 \times 4$ өлшемді шаршы шығатындай етіп, $A, B$ фигураларының әрқайсысын, сәйкесінше, қандай да $l_A, l_B$ түзулеріне қатысты симметриялап, кейін $C$ фигурасын бұрыңыз. $l_A, l_B$ түзулерін және $C$-ның бұру центрін көрсетіп, осы $A, B$ және $C$-ға қолданылған операциялардан алынған фигураларды салып көрсетіңіз.


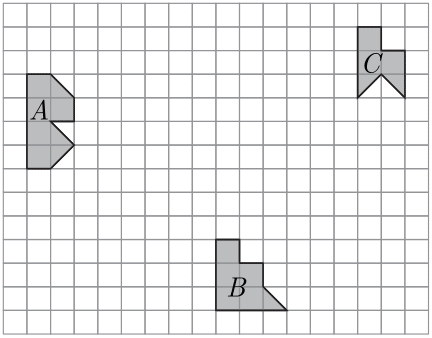
комментарий/решение(1)
Есеп №2. Қабырғасы 20-ға тең $ABCD$ шаршысының $A$ төбесінен жарық сәуле шығып, сәйкесінше, $BC, CD, DA$ қабырғаларынан шағылып, кейін $AB$ қабырғасының ортасына жетеді. Осы сәуленің жүріп өткен жолының ұзындығы нешеге тең?


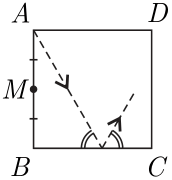
комментарий/решение(1)
Есеп №3. Дөңес $ABCD$ төртбұрышының ішінде $T$ нүктесі белгіленген. $AT$ кесіндісінен $DT = BC$ және $\angle TSD = 90^\circ$ болатындай $S$ нүктесі алынған. Егер $\angle DTA + \angle TAB + \angle ABC = 180^\circ$ болса, $AB + ST \geqslant CD + AS$ екенін дәлелдеңіз. (Ұйымдастырушылар есепті қосымша $BC>AD$ шартымен шешу керектігін кеш хабарлады.)
комментарий/решение(4)
Есеп №4. Іштей сызылған $n$-бұрыштың ($n > 3$) бір төбесінен барлық диагоналдарды жүргізіп, көпбұрышты ${n-2}$ үшбұрышқа бөлген. Осы үшбұрыштардың ең көп дегенде нешеуі тең үшбұрыштар бола алады? (Іштей сызылған $n$-бұрыш деп, төбелері бір шеңберде жататын көпбұрышты айтамыз.) (Бұл есептің берілгені түпнұсқадан ерекшеленеді, себебі ол қате аударылған.)
комментарий/решение(1)
Есеп №5. $Y, Z$ нүктелері сүйір бұрышты $ABC$ үшбұрышына сырттай сызылған шеңбердің $BC$-ның кіші доғасындағы нүктелер (мұнда $Y$ нүктесі $BZ$ кіші доғасында жатыр). $X$ нүктесі үшін $\triangle ABC$ және $\triangle XYZ$ үшбұрыштары ұқсас және $A, X$ нүктелері $YZ$ түзуінің бір жағында жатыр. $XY, XZ$ түзулері $AB, AC$ қабырғаларын, сәйкесінше, $E, F$ нүктелерінде қияды. $BY$ және $CZ$ түзулері $K$ нүктесінде қиылысады. $AEF$ және $KBC$ үшбұрыштарына сырттай сызылған шеңберлердің қиылысу нүктелерінің бірі $KX$ түзуінде жатқанын дәлелдеңіз.
комментарий/решение(2)