8-я олимпиада им. Шалтая Смагулова, 6 класс, 1 тур

Задача №1. На трёх полках лежат 342 книг. На первой полке книг в 2 раза больше, чем во второй, а на третьей в 3 раза больше, чем во второй. Сколько книг на третьей полке?
комментарий/решение(2)

Задача №2. Если из двух городов одновременно навстречу друг другу выехали бы первый и второй автомобили со скоростями 40 км/ч и 65 км/ч соответственно, то они встретились бы через 240 минут. Через сколько минут они встретились бы, если выехал бы только первый автомобиль, а второй стоял бы на месте?
комментарий/решение(1)

Задача №3. В классе 25 учеников. 13 из них посещают кружок домбры, а 18 — кружок математики. В классе только Жалкаубек не посещает ни один кружок. Сколько учеников посещают оба кружка?
комментарий/решение(1)

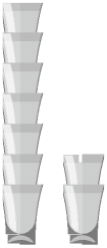
Задача №4. На рисунке стаканы вставлены друг в друга. Стопка из семи стаканов имеет высоту 38 см, а стопка из двух стаканов — 18 см. Какую высоту (в сантиметрах) имеет стопка из 5 стаканов?

комментарий/решение

Задача №5. Вычислите: $6,\!563\cdot 5,\!573+4,\!427\cdot 5,\!437+6,\!563\cdot 4,\!427+5,\!437 \cdot5,\!573$.
комментарий/решение

Задача №6. Учителю 32 года, а в его классе 20 учеников. Если средний возраст всех 21 присутствующих в классе, на момент преподавания, равен 12 лет, то чему равен (в годах) средний возраст 20 учеников?
комментарий/решение(1)

Задача №7. Найдите $x$ из уравнения: $1 + 9 : (1 - 8 : (1 + 4 : (1 - 6 : (1 + 5 : (1 - 4 : x))))) = 34.$
комментарий/решение

Задача №8. Для натуральных чисел $a$, $b$ и $c$ выполнены цепочки неравенств $\frac{1}{3}<\frac{a}{8}<\frac{2}{5}<\frac{b}{7}<\frac{1}{2}<\frac{4}{c}<\frac{3}{5}$. Найдите сумму $a+b+c$.
комментарий/решение

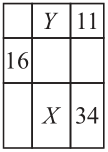
Задача №9. На рисунке прямоугольник периметра 100 разделён на 9 меньших прямоугольников. В пяти из них указаны их периметры. Найдите значение разности периметров $X-Y$.

комментарий/решение

Задача №10. Асану на олимпиаде дали 10 двухбалльных легких и 10 трехбалльных сложных задач. После олимпиады, на вопрос друзей «Сколько легких и сколько сложных задач ты решил?», он ответил следующим образом. Первому другу: 8 легких и 6 сложных, второму: 7 легких и 4 сложных, третьему: 7 легких и 7 сложных. Известно, что каждому другу на один вопрос ответил верно, на другой – солгал. Сколько баллов Асан набрал на этой олимпиаде?
комментарий/решение

Задача №11. Сумму $0,\!(87)+0,\!(78)$ представили в виде неправильной несократимой дроби $\frac{m}{n}$, то есть $0,\!(87)+0,\!(78) = \frac{m}{n}$ (здесь $m$ и $n$ такие натуральные числа, что НОД$(m,n)=1$). Найдите $m+n$. (Здесь первые дроби — периодические. Примером такой дроби является число $\frac{2}{3}=0,\!(6)$.)
комментарий/решение

Задача №12. Дана последовательность чисел: $\frac{1}{3}$, $\frac{7}{9}$, $\frac{17}{19}$, $\frac{31}{33}$, $\frac{49}{51}$, $\frac{71}{73}$, $\frac{m}{n}$. Определив закономерность в последовательности, найдите произведение $m\cdot n$. Здесь $m$ и $n$ такие натуральные числа, что НОД$(m,n)=1$.
комментарий/решение

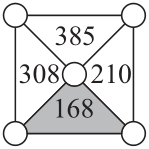
Задача №13. На рисунке в кружочки вписаны числа 4, 5, 6, 7 и 11. Внутри каждого треугольника записали число, равное произведению чисел в вершинах этого треугольника. Чему равна сумма чисел в вершинах серого треугольника?

комментарий/решение

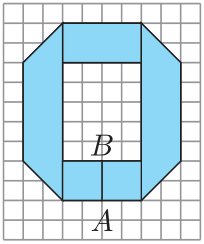
Задача №14. Асан, сгибая прямоугольную полоску, сделал букву O (на рисунке сторона клетки равна 1, а $AB$ — линия склейки концов полоски). Чему был равен периметр полоски изначально?

комментарий/решение

Задача №15. В круговом шахматном турнире участвуют $n$ шахматистов, и каждый участник играет с каждым из остальных один раз. На турнире всего было сыграно больше 100, но меньше 120 игр. Найдите $n$.
комментарий/решение

Задача №16. Операцией дублирования $s(x)$ числа $x$, назовём приписывание этого же числа к самому числу. Например, $s(123)=123123$. Сумма двухзначных чисел $a$ и $b$ равна 108. Найдите $s(a)+s(b)$.
комментарий/решение(1)

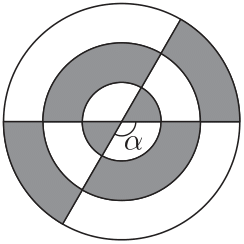
Задача №17. На рисунке даны три круга радиусов 10, 20 и 30 см, имеющие общий центр, и $\alpha=120^\circ$. Скольким см$^2$ равна общая площадь закрашенных частей? (Считайте, что $\pi=3,\!14$.)

комментарий/решение

Задача №18. В стране имеется три города: $A$, $B$, $C$. Из города $A$ в город $C$ по дорогам можно попасть только через город $B$. Какое наименьшее число дорог может быть в стране, если из $A$ в $C$ можно попасть 286 способами?
комментарий/решение

Задача №19. Шестизначное число начинается с цифры 2. Если эту цифру перенести в конец числа, то число увеличится в три раза. Найдите сумму цифр этого шестизначного числа.
комментарий/решение

Задача №20. Сколько общих членов имеют последовательности чисел видов 2, 5, 8, $\ldots$, 200 и 1, 5, 9, $\ldots$, 201?
комментарий/решение