Юниорская олимпиада по математике. Районный этап. 2024-2025 учебный год. 7 класс.
Задача №1. Полный бидон с молоком весит 7 кг, а наполенный наполовину 4 кг. Сколько весит пустой бидон?
A) 1 кг
B) 0,5 кг
C) 1,5 кг
D) 2 кг
E) Анықтау мүмкін емес/ нельзя определить
комментарий/решение
A) 1 кг
B) 0,5 кг
C) 1,5 кг
D) 2 кг
E) Анықтау мүмкін емес/ нельзя определить
комментарий/решение
Задача №2. Марат задумал простое трехзначное число, все цифры которого различные. На какую цифру оно может оканчиваться, если его последняя цифра равна сумме первых двух.
A) 1
B) 3
C) 5
D) 7
E) Анықтау мүмкін емес/ нельзя определить
комментарий/решение
A) 1
B) 3
C) 5
D) 7
E) Анықтау мүмкін емес/ нельзя определить
комментарий/решение
Задача №3. После двукратного повышения цены на 25$\%$ банка сока стала стоит 3750 тг. Какова была ее исходная цена?
A) 1600
B) 1875
C) 2000
D) 2200
E) 2400
комментарий/решение
A) 1600
B) 1875
C) 2000
D) 2200
E) 2400
комментарий/решение
Задача №4. Найдите количество различных натуральных делителей числа $6^{15} \cdot 21^7$.
A) 105
B) 225
C) 2225
D) 2754
E) 2944
комментарий/решение
A) 105
B) 225
C) 2225
D) 2754
E) 2944
комментарий/решение
Задача №5. Площадь белой зоны на рисунке равна 6 см$^2$. Какова площадь темной зоны?
A) 3
B) 4
C) 6
D) 9
E) 12
комментарий/решение
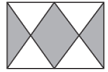
A) 3
B) 4
C) 6
D) 9
E) 12
комментарий/решение
Задача №6. Какой цифрой оканчивается разность $9^{1972}-7^{1972}$?
A) 0
B) 1
C) 2
D) 3
E) 4
комментарий/решение
A) 0
B) 1
C) 2
D) 3
E) 4
комментарий/решение
Задача №7. Сумма уменьшаемого, вычитаемого и разности равна 2000. Найдите уменьшаемое.
A) 888
B) 999
C) 1000
D) 1001
E) 1002
комментарий/решение
A) 888
B) 999
C) 1000
D) 1001
E) 1002
комментарий/решение
Задача №8. Вычислите: $\frac{3}{1 \cdot 2}+\frac{3}{2 \cdot 3}+\frac{3}{3 \cdot 4}+\cdots+\frac{3}{2024 \cdot 2025}.$
A) $\frac{2024}{2025}$
B) $1 \frac{4}{2025}$
C) $1 \frac{624}{675}$
D) $1 \frac{374}{675}$
E) $2 \frac{674}{675}$
комментарий/решение
A) $\frac{2024}{2025}$
B) $1 \frac{4}{2025}$
C) $1 \frac{624}{675}$
D) $1 \frac{374}{675}$
E) $2 \frac{674}{675}$
комментарий/решение
Задача №9. В одной комнате сидят 9 человек и их средний возраст 25 лет. В другой комнате сидят 11 человек и их средний возраст 45 лет. Каков средний возраст всех 20 человек?
A) 40
B) 36
C) 35
D) 32
E) 30
комментарий/решение
A) 40
B) 36
C) 35
D) 32
E) 30
комментарий/решение
Задача №10. Вычислите: $3 \cdot 6 \cdot 9 \cdot 12 + 81.$
A) 1625
B) 1825
C) 2025
D) 2225
E) 2425
комментарий/решение
A) 1625
B) 1825
C) 2025
D) 2225
E) 2425
комментарий/решение
Задача №11. Найти наименьшее натуральное число, половина которого есть пятая степень.
A) 512
B) 128
C) 64
D) 32
E) 243
комментарий/решение
A) 512
B) 128
C) 64
D) 32
E) 243
комментарий/решение
Задача №12. Какой угол образуют стрелки часов в 2 ч 20 мин?
A) $30^\circ$
B) $35^\circ$
C) $40^\circ$
D) $45^\circ$
E) $50^\circ$
комментарий/решение
A) $30^\circ$
B) $35^\circ$
C) $40^\circ$
D) $45^\circ$
E) $50^\circ$
комментарий/решение
Задача №13. Найдите сумму цифр числа $x$ в уравнении $\frac{2}{73}=\frac{1}{60}+\frac{1}{219}+\frac{1}{292}+\frac{1}{x}.$
A) 9
B) 12
C) 14
D) 15
E) 16
комментарий/решение
A) 9
B) 12
C) 14
D) 15
E) 16
комментарий/решение
Задача №14. Какова сумма углов, отмеченных на рисунке?
A) 1200
B) 1500
C) 1800
D) 2700
E) 3600
комментарий/решение
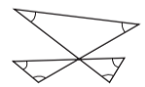
A) 1200
B) 1500
C) 1800
D) 2700
E) 3600
комментарий/решение
Задача №15. На даче поселились пятеро мальчиков: Арман, Багдат, Марат, Галымжан и Дамир. Все были разного возраста: одному 1 год, другому 2 года, остальним 3, 4, и 5 лет. Марат был самым маленьким, Дамиру было столько лет, сколько Арман и Галымжану вместе. Сколько лет Багдату.
A) 4
B) 2
C) 3
D) 5
E) 1
комментарий/решение
A) 4
B) 2
C) 3
D) 5
E) 1
комментарий/решение
Задача №16. В числовом ребусе $\text{КОКА} + \text{КОЛА} = \text{ВОДА}$ дайдите Д.
A) 0
B) 1
C) 2
D) 3
E) 4
комментарий/решение
A) 0
B) 1
C) 2
D) 3
E) 4
комментарий/решение
Задача №17. После 7 стирок хозяйственного мыла уменьшился вдвое по длине, ширине и высоте. На сколько стирок его еще хватит?
A) 2
B) 1
C) 7
D) 4
E) 8
комментарий/решение
A) 2
B) 1
C) 7
D) 4
E) 8
комментарий/решение
Задача №18. Сколько всего пар натуральных чисел $(x, y) \in \mathbb{N}$ удовлетворяет условию $2x+1 \vdots y$, $2y+1 \vdots y$?
A) 1
B) 2
C) 3
D) 4
E) 5
комментарий/решение
A) 1
B) 2
C) 3
D) 4
E) 5
комментарий/решение
Задача №19. Из операции ниже найдите требуемое значение.
A) $3 \cdot 2^4$
B) $2^{9}$
C) $2^{12}$
D) $2^{20}$
E) $2^{5}$
комментарий/решение
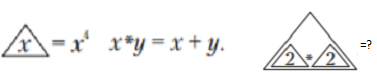
A) $3 \cdot 2^4$
B) $2^{9}$
C) $2^{12}$
D) $2^{20}$
E) $2^{5}$
комментарий/решение
Задача №20. На гранях кубика расставлены числа от 1 до 6. Кубик бросили два раза. В первый раз сумма чисел на четырех боковых гранях оказалась равна 12, во второй 15. Какое число написано на грани, противоположной той, где написано 3?
A) 2
B) 3
C) 4
D) 5
E) 6
комментарий/решение
A) 2
B) 3
C) 4
D) 5
E) 6
комментарий/решение
Задача №21. Какую цифру надо вставить вместо $x$, чтобы $567x80$ делилось на 90?
A) 0
B) 2
C) 3
D) 4
E) 1
комментарий/решение
A) 0
B) 2
C) 3
D) 4
E) 1
комментарий/решение
Задача №22. Найти разность знаменателя и чиситля дроби. Равную $\frac{399}{1064}$, зная, что сумма числителя и знаменателя составляет куб простого числа.
A) 1
B) 2
C) 3
D) 4
E) 5
комментарий/решение
A) 1
B) 2
C) 3
D) 4
E) 5
комментарий/решение
Задача №23. На плоскости проведены 4 прямые. Пусть $n$ — количество их точек пересечения. Чему $n$ не может быть равно?
A) 0
B) 2
C) 3
D) 5
E) 6
комментарий/решение
A) 0
B) 2
C) 3
D) 5
E) 6
комментарий/решение
Задача №24. Сколько натуральных чисел, не делящихся ни на 3, на на 7, ни на 11, имеется среди первых 10000 натуральных чисел?
A) 5105
B) 5205
C) 5305
D) 5405
E) 5505
комментарий/решение
A) 5105
B) 5205
C) 5305
D) 5405
E) 5505
комментарий/решение
Задача №25. У автомобиля новые шины. Шина на заднем колесе выдерживает пробег 16000 км, а на переднем 24000 км. Какой максимальный пробег можно осуществить на этих колесах.
A) 18200
B) 18400
C) 22200
D) 19200
E) 19800
комментарий/решение
A) 18200
B) 18400
C) 22200
D) 19200
E) 19800
комментарий/решение
Задача №26. Из трех следующих утверждений два верны, а одно неверно: 1) $A+51$ есть точный квадрат. 2) последняя цифра числа $A$ есть единица. 3) $A-38$ есть точный квадрат. Найдите сумму цифр числа $A$.
A) 21
B) 21
C) 23
D) 24
E) 25
комментарий/решение
A) 21
B) 21
C) 23
D) 24
E) 25
комментарий/решение
Задача №27. Два всадника выезжают одновременно из А и В навстречу друг другу. После встречи первый прибывает в В через 27 мин, а второй в А через 12 мин. За какое время проехал первый всадник АВ?
A) 30 мин
B) 35 мин
C) 40 мин
D) 45 мин
E) 48 мин
комментарий/решение
A) 30 мин
B) 35 мин
C) 40 мин
D) 45 мин
E) 48 мин
комментарий/решение
Задача №28. Отец с двумя сыновями отправились навестить бабушку, которая живет в 33км от города. У отца есть мотороллер, скорость которого 25 км/ч, а с пассажиром 20 км/ч (двух пассажиров на мотороллере перевозить нельзя). Каждый из братьев идет по дороге со скоростью 5 км/ч. За какое минимальное время все трое доберуться до бабушки?
A) 3
B) 3,5
C) 4,5
D) 5
E) 5,5
комментарий/решение
A) 3
B) 3,5
C) 4,5
D) 5
E) 5,5
комментарий/решение
Задача №29. Выполняется равенство $\overline{x x x x}-\overline{y y}=x(\overline{x x})^2$, где $x, y$ цифры. Чему равна сумма $x+y$?
A) 5
B) 11
C) 7
D) 13
E) 9
комментарий/решение
A) 5
B) 11
C) 7
D) 13
E) 9
комментарий/решение
Задача №30. Студент за 5 лет учебы сдал 31 экзамен. В каждом следующем году он сдавал больше экзаменов, чем в предыдущем. На V курсе экзаменов втрое больше, чем на І курсе, сколько экзаменов на IV курсе?
A) 7
B) 4
C) 5
D) 6
E) 8
комментарий/решение
A) 7
B) 4
C) 5
D) 6
E) 8
комментарий/решение