Математикадан 49-шы халықаралық олимпиада, 2008 жыл, Мадрид

$ABC$ сүйірбұрышты үшбұрышының биіктіктерінің қиылысу нүктесі $H$ болсын. Центрі $BC$ қабырғасында орналасқан $H$ нүктесі арқылы өтетін шеңбер $BC$ түзуін ${{A}_{1}}$ және ${{A}_{2}}$ нүктелерінде қияды. Дәл сондай центрі $CA$ қабырғасының ортасында болатын $H$ нүктесі арқылы өтетін шеңбер $CA$ түзуін ${{B}_{1}}$ және ${{B}_{2}}$ нүктелерінде қияды, ал центрі $AB$ қабырғасының ортасында болатын $H$ нүктесі арқылы өтетін шеңбер $AB$ түзуін ${{C}_{1}}$ және ${{C}_{2}}$ нүктелерінде қияды. ${{A}_{1}}$, ${{A}_{2}}$, ${{B}_{1}}$, ${{B}_{2}}$, ${{C}_{1}}$, ${{C}_{2}}$ нүктелері бір шеңбердің бойында жататынын дәлелдеңіздер.

Комментарий/решение

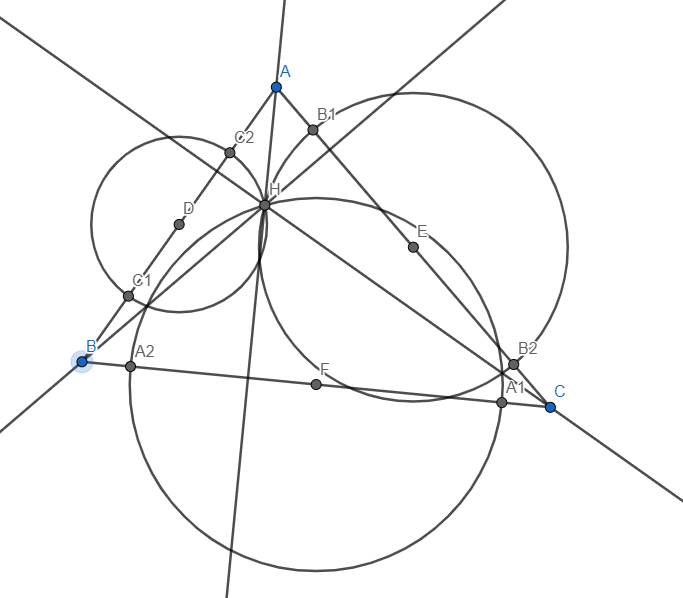
Пусть $\omega_1, \omega_2, \omega_3$ окружности с диаметром на $BC, AB, AC$ соответственно. На самом деле нам достаточно показать концикличность следующих четверок точек: $C_1C_2B_1B_2$, $C_1C_2A_1A_2$, $A_1A_2B_1B_2$

(i)$C_1C_2B_1B_2$

Пусть $D, E, F$ середины $AC, AB, BC$. Для вписанности нам достаточно показать что $Pow(A, \omega_3) = Pow(A, \omega_2)$. То есть $A$ - должна лежать на радикально оси этих окружностей. Зная что $H$ лежит на одном из пересечений окружностей, $AH$ должна является искомой радикальной осью. Соединим $D$ и $E$, очевидно $AH \perp DE$, причем $D$ и $E$ являются центром обоих окружностей, но прямая перпендикулярная отрезку соединяющего центры двух окружностей, проходящая через одну из точек пресечения, является радикальной осью.

Для оставшихся точек $C_1C_2A_1A_2$, $A_1A_2B_1B_2$, доказательство аналогичны.

Нурс аби мощь