Математикадан аудандық олимпиада, 2015-2016 оқу жылы, 11 сынып

$ABCD$ параллелограммының диагональдары $O$ нүктесінде қиылысады, ал $\angle DAC$ және $\angle DBC$ бұрыштарының биссектрисалары $T$ нүктесінде қиылысады. $\overrightarrow{TD}+\overrightarrow{TC}=\overrightarrow{TO}$ екені белгілі. $ABT$ үшбұрышының барлық бұрыштарын табыңыз.

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Ответ. Все углы треугольника $ABT$ равны $60^\circ$.
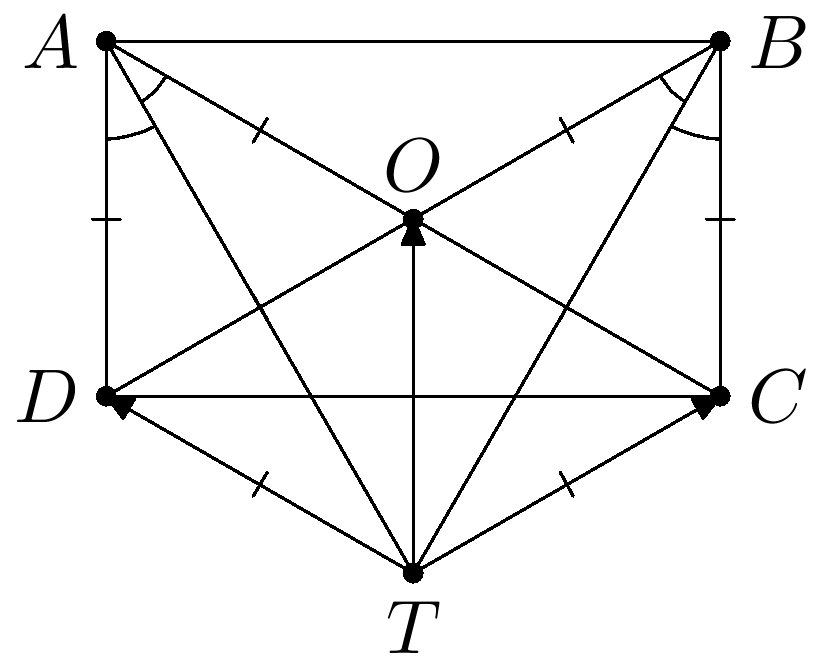
Решение. Равенство $\overrightarrow{TD}+\overrightarrow{TC}=\overrightarrow{TO}$ как раз удовлетворяет правилу параллелограмма. Получается, что $DOCT$ — параллелограмм и точка $T$ лежит снаружи параллелограмма. $\angle DTA = \angle TAC$. Но так как по условию $\angle TAC = \angle TAD$, то $DA=DT$. Аналогично, $BC=CT$. Но так как $AD=BC$, получим $DO=TC=BC=AD=DT=OC$. Как видим, половины диагоналей параллелограмма $ABCD$ равны, то есть $ABCD$ — прямоугольник, причем углы треугольников $DAC$ и $DBC$ равны $60^\circ$. Тогда $\angle TAB = \angle TAC+\angle CAB= 30^\circ+30^\circ=60^\circ$, и аналогично, $\angle TBA=60^\circ$.