Геометриядан Иран олимпиадасы, 2017 жыл, 3-ші лига (11-12 сыныптар)

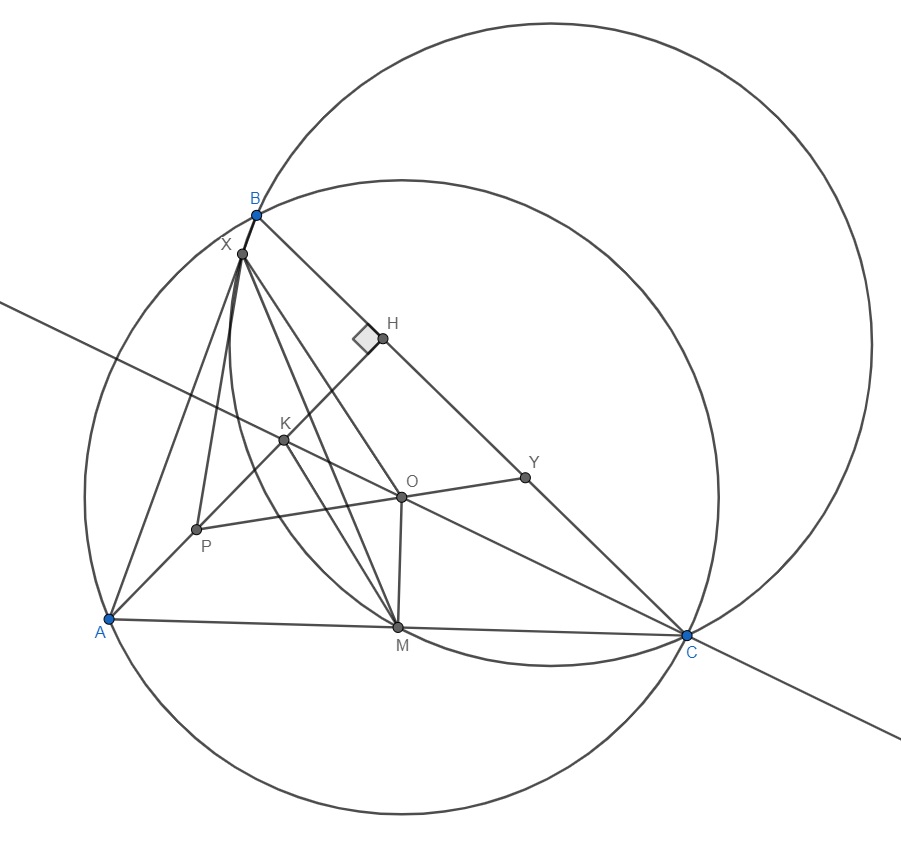
$O$ нүктесі $ABC$ үшбұрышына сырттай сызылған шеңбердің центрі. $CO$ түзуі үшбұрыштың $A$ төбесінен түсірілген биіктікті $K$ нүктесінде қияды. $P$ және $M$ нүктелері сәйкесінше $AK$ және $AC$ кесінділерінің орталары. Егер $PO$ түзуі $BC$-ны $Y$, ал $BCM$ үшбұрышына сырттай сызылған шеңбер $AB$-ны екінші рет $X$ нүктесінде қиса, $BXOY$ төртбұрышының шеңберге іштей сызылғанын дәлелдеңіздер.

Комментарий/решение

Докажем что $XPO, \ AXM$ подобны это докажет что $\angle XOP = \angle ABC$ ($BXOY$ вписанный), для этого докажем что $AXP,XOM$ подобны так как $\angle OMX = 90-\angle AMX = 90 - \angle ABC = \angle XAP$ то есть надо доказать что $\dfrac{AX}{AP}=\dfrac{2AX}{AK}=\dfrac{MX}{MO}$ выражая $AK=\dfrac{ACcos(\angle B)}{sin(\angle B+\angle C)}, \ AX=\dfrac{ACsin(\angle B)}{2sin( \angle C)}, \ XM=\dfrac{ACsin(\angle A)}{2sin(\angle C)} , \ MO=\dfrac{ACcos(\angle B)}{2sin(\angle B)}$

Подставляя , откуда $sin(B+C)=sin(A)$ что верно.