Республиканская олимпиада по математике, 2018 год, 9 класс

На боковой стороне $CD$ трапеции $ABCD$ нашлась точка $M$ такая, что $BM=BC$. Пусть прямые $BM$ и $AC$ пересекаются в точке $K$, а прямые $DK$ и $BC$ — в точке $L$. Докажите, что углы $BML$ и $DAM$ равны. ( М. Кунгожин )

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     В решении будем пользоваться тем фактом, что если диагонали четырехугольника $XYZT$ пересекаются в точке $O$, то $XY \parallel ZT$ тогда, и только тогда, когда $XO/OZ=YO/OT$.
Пусть прямая, проходящая через $A$ и параллельная $CD$, пересекает прямую $BM$ в точке $E$. Тогда, $\angle AEM=\angle EMC=\angle MCB=180^\circ-\angle ADC=\angle DAE$. Значит, $AEMD$ --- равнобокая трапеция, то есть $\angle DAM=\angle DEM$. Также имеем: $EK/KM=AK/KC=DK/DL$. Следовательно, $ED \parallel LM$, откуда $\angle DEM = \angle BML$.

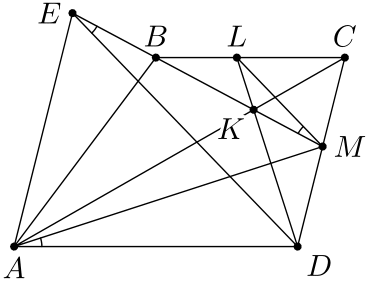
Пусть $E \in AM \cap BC$ , $\angle ADC = D$ тогда $\angle DAM = \angle BEM$ , запишем теорему Менелая для секущей $AC$ треугольника $MBE$ и для секущей $DL$ треугольника $BMC$ получаем соответственно $\dfrac{CE}{CB } \cdot \dfrac{BK}{MK} \cdot \dfrac{AM}{AE} = 1$ и $\dfrac{CL}{BL} \cdot \dfrac{BK}{MK} \cdot \dfrac{DM}{CD}=1$. Так как $\dfrac{AE}{AM} = \dfrac{CD}{DM}$ получаем что $\dfrac{CE}{CB} = \dfrac{CL}{BL}$ которую можно записать как $\dfrac{\sin(D+ \angle BML)}{sin \angle BML} = \dfrac{\sin(D+\angle DAM)}{sin \angle DAM}$ (пользуясь тем что $BM=BC$) откуда $\angle DAM = \angle BML$ или $CM$ биссектриса угла $EML$.

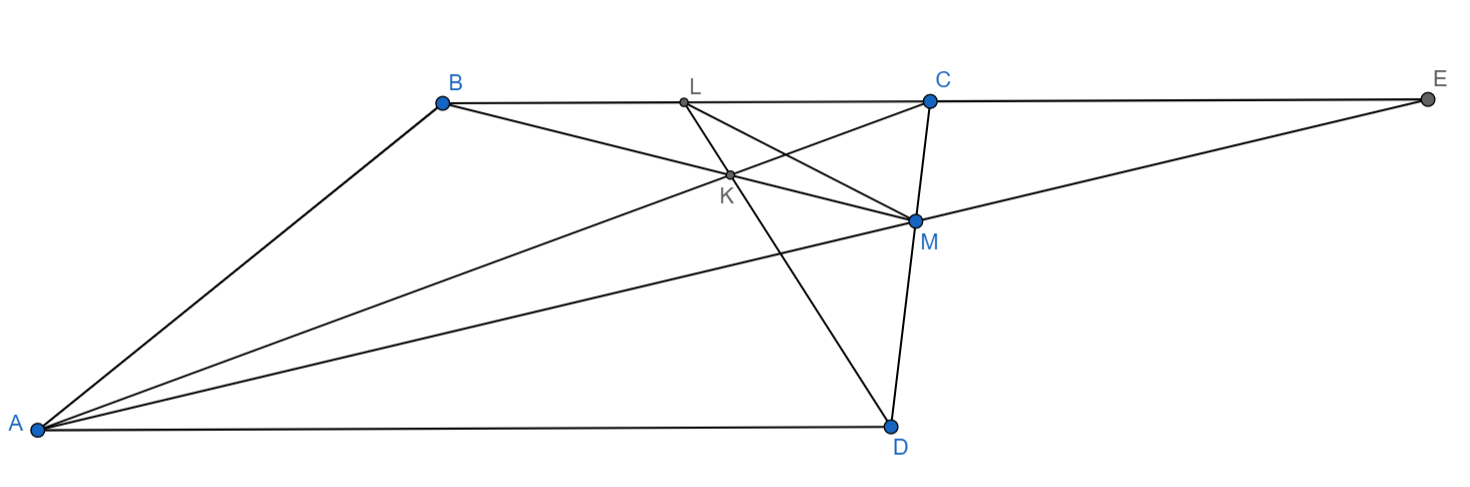
Пусть $AM$ пересекает $BC$ в точке $E,$ а $BM$ пересекает $AD$ в точке $F.$ Достаточно доказать, что $\angle BML=\angle BEM,$ что равносильно с

$$BL\cdot BE=BM^2\iff \dfrac{BL}{BC}=\dfrac{BC}{BE}.$$

Поскольку $BC\parallel AF,$ то $\dfrac{BL}{BC}=\dfrac{FD}{AF}.$

Поскольку $BE\parallel AF,$ то $\dfrac{BC}{BE}=\dfrac{FD}{AF},$ откуда следует требуемое.