Математикадан облыстық олимпиада, 2019 жыл, 9 сынып


Центрлері сәйкесінше $O_1$ және $O_2$ нүктелері болатын $\Gamma_1$ және $\Gamma_2$ шеңберлері $A$ және $B$ нүктелерінде қиылысады. $O_1A$ түзуі $\Gamma_2$ шеңберін екінші рет $C$ нүктесінде, ал $O_2A$ түзуі $\Gamma_1$ шеңберін екінші рет $D$ нүктесінде қиып өтеді. $AD$-ға параллель $\ell$ түзуі $\Gamma_1$ шеңберін $B$ және $E$ нүктелерінде қиып өтеді. Егер $O_1 A\parallel DE$ екені белгілі болса, $CD \perp O_2C$ болатынын дәлелдеңдер.
посмотреть в олимпиаде

Комментарий/решение:

Комментарии от администратора Комментарии от администратора №1.    
Решение. Как известно, прямая, соединяющая центры окружностей, перпендикулярна их общей хорде. Также известно, что концы двух параллельных хорд окружности являются вершинами равнобокой трапеции. Следовательно, $AB \perp O_1O_2$ и $ ABED$ — равнобокая трапеция (см. рис. ниже). Так как $ED \parallel O_1A$, то из симметрии, относительно серединных перпендикуляров $AD$ и $EB$, следует параллельность ${DO_1 \parallel AB}$, то есть $\angle DO_1O_2 =90^\circ$.


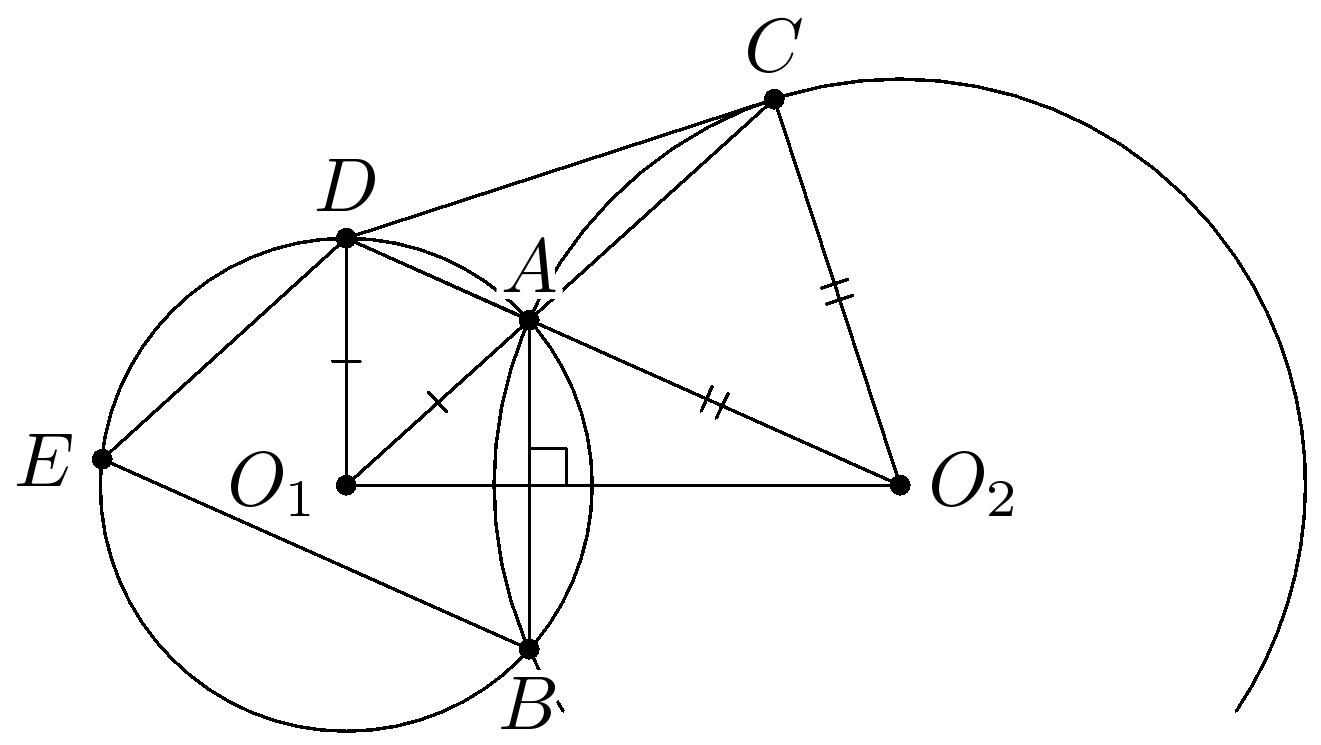
   Равнобедренные треугольники $ACO_2$ и $ADO_1$ подобны, так как у них имеются равные вертикальные углы при основаниях. Поэтому $\angle O_1DO_2=\angle O_1CO_2$, то есть $O_2CDO_1$ — вписанный четырехугольник. Осталось заметить, что $\angle DCO_2=180^\circ-\angle DO_1O_2=180^\circ-90^\circ=90^\circ.$