6-я международная Иранская олимпиада по геометрии, 2019 год, вторая лига, 9-10 классы
Комментарий/решение:
Задача эквивалентна параллельным переносом, такой задаче:
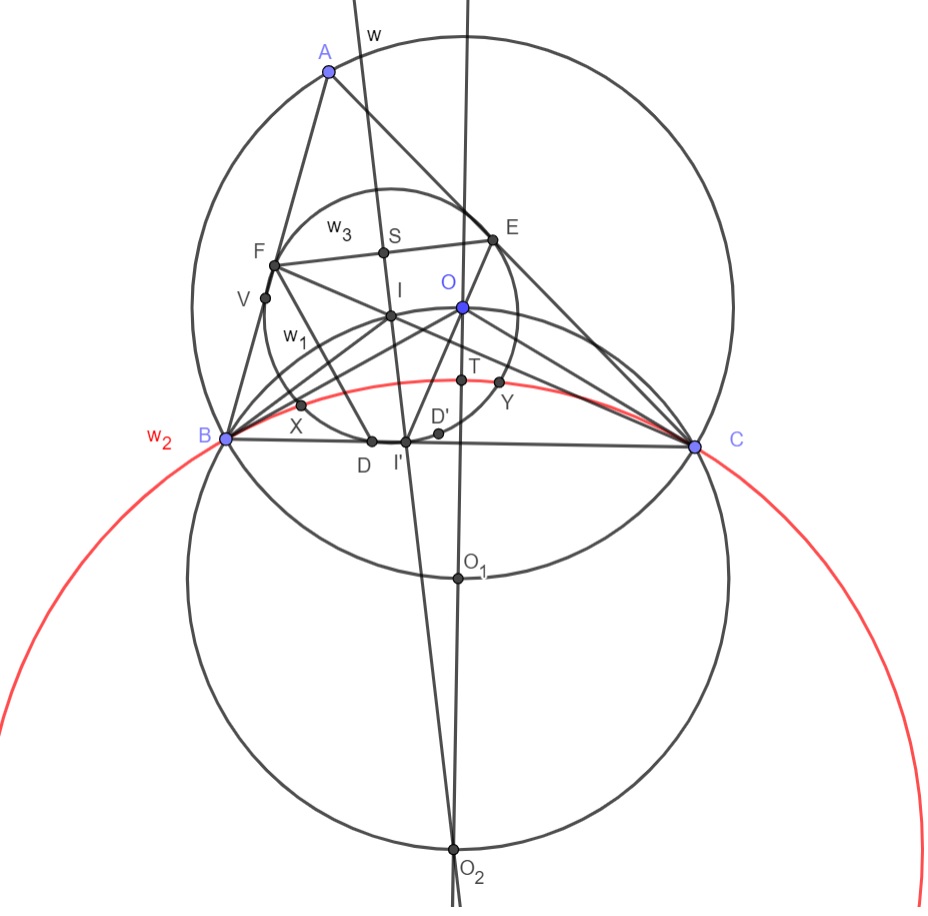
Пусть $(O, \ w)$ окружность описанная около $ABC$, так же $(O_{1}, w_{1})$ окружность описанная около $BOC$ тогда из условия $w=w_{1}$ и $O_{2} \in OO_{1} \cap w_{1}$.
Пусть $w_{2}$ окружность с радиусом $O_{2}B=O_{2}C$ проведем биссектрису $l$ из точки $A$ и пусть $M \in l \cap w_{1}$ ,тогда $\angle BMC = 180^{\circ}-\angle BAC = 120^{\circ}$ тогда $M=I$ где $I$ - инцентр, пусть $I' \in O_{2}I \cap BC$ тогда по свойству инверсий, относительно $w_{3}$ луч $BC$ образ $w_{1}$ так как $\angle OIO_{2} = 90^{\circ}$ так как $OO_{2}$ диаметр, откуда $\angle OIC = \angle OBC = 30^{\circ}$ значит $\angle CIO_{2} = 60^{\circ}$ следовательно $IO_{2}$ биссектриса $\angle BIC$. По условию $CF, BE$ биссектрисы, тогда $\angle FIB = 60^{\circ}$ тогда $\Delta BII' = \Delta BIF$ по двум углам и стороне $BI$ откуда $BI'=BF$ и $IF=II'$ аналогично $IE=II'$ и $CI'=CE$ учитывая что $\angle FII' = \angle EII' = 120^{\circ}$ значит $FEI'$ правильный откуда $\angle BFE = \angle BI'E$ . Пусть $w_{3}$ окружность с центром $I$ и $R=II'$. Пусть $D \in w_{3} \cap BC$ тогда $\angle BFD = \angle BFE - \angle DFE = \angle BI'E - \angle EI'C = 180^{\circ} - 2 \angle EI'C = \angle ACB$ то есть $FDCA$ вписанный, откуда $\angle AFE = \angle DFE$ аналогично $\angle AEF = \angle FED$ тогда $AF=DF, \ AE=DE$ то есть $D$ симметрична $А$ относительна $FE$.
Пусть $X,Y \in w_{2} \cap w_{3}$ тогда $IX=IY, \ O_{2}X = O_{2}Y$ тогда $XY || FE$ рассмотрим симметричную точку $D'$ относительно $O_{2}I$ к точке $D$ тогда $D' \in w_{3}$ и $FD' || AC, \ ED' || AB$ тогда суть задачи доказать что $\angle PAQ = \angle BD'C > 150^{\circ}$, если $T \in O_{1}O_{2} \cap w_{2}$ тогда $D'$ лежит внутри сегмента $BTC$ но $\angle BTC = 180^{\circ}-\dfrac{\angle BO_{2}C}{2} = 150^{\circ}$ значит $\angle PAQ = \angle BD'C \geq \angle BTC = 150^{\circ}$

Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.